Salience, Common Tones, and Middleground Dissonance in the Fourth Chorus of Brad Mehldau’s Improvisation on “All the Things You Are”

Rich Pellegrin

Abstract

This article addresses the analytical fault line between Schenkerian and Salzerian approaches to tonal jazz through an analysis of a Brad Mehldau improvisation on “All the Things You Are.” Special attention is given to the usage of common tones, which often work against the resolving tendencies of unstable chord tones but create their own large-scale structure. The essay engages with work of Fred Lerdahl and is informed by my model, Stable Norms and Salient Deviations (SNSD).

View PDF
Return to Volume 36

Keywords and phrases: jazz, improvisation, Felix Salzer, Heinrich Schenker, Fred Lerdahl, stability, salience, Brad Mehldau, rhythmic analysis

This essay examines the relationship between stability and salience in the fourth chorus of Brad Mehldau’s improvisation on “All the Things You Are,” that which appears on his 1999 live album Art of the Trio, Volume 4: Back at the Vanguard.¹ My analysis demonstrates how middleground common tones that are salient, but often unstable, combine to form plateaus and ascending linear motions. These lines and plateaus work against the resolutions implied by the descending-fifths harmonic motion, until the passage resolves and reconnects with the stability of the underlying form.²

Analytical discourse often involves the issue of salience, whether explicitly or implicitly. My use of the word “salience” derives from a rich corpus of studies investigating the relationship between rhythmic analysis and prolongational analysis, including writings of Fred Lerdahl and Ray Jackendoff (1977, 1983, 1983/1984), Lerdahl (1989, 2001), Carl Schachter ([1976] 1999, [1980] 1999, [1987] 1999), and William Rothstein (1981, 1989, 1990).³ The work of these scholars developed concurrently, and their ideas cross-fertilized and are generally consistent with one another.

Salience may be roughly considered as a measure of how perceptually prominent a note is within a given texture. In this context, “salient” does not mean “important,” which dictionaries sometimes list as one of its definitions.⁴ The concept of salience encompasses a wide range of parameters, which may be broadly categorized as follows: first, those that are commonly studied using hierarchical levels, such as meter and grouping; second, those that are less frequently (or less independently) examined in such fashion, such as register, timbre, and dynamics; and third, parallelism (i.e., repetition).⁵ Salience is often affected significantly by changes in a given parameter. For example, in a subito piano passage, the change of loudness creates an accent that may cause the beginning of the section to be heard as a boundary in the grouping structure.

In this literature, salience is distinguished from stability, which is more directly related to pitch space, tonal closure, and prolongation. Lerdahl and Jackendoff (1983, 117–118) write:

Broadly, the relative stability of a pitch-event can be thought of in terms of its relative consonance or dissonance. For example, a local consonance is more stable than a local dissonance, a triad in root position is more stable than its inversion, the tonic is the most stable harmony, the relative stability of two chords is a factor of the relative closeness to the tonic (or the local tonic) of their roots on the circle of fifths, conjunct linear connections are more stable than disjunct ones, and so forth.  

Within a jazz context, where extended harmonic structures are typical, the upper chord tones (sevenths and extensions) are relatively unstable, the lower chord tones are more stable, and the chord root is the most stable.⁶ 

Musical events are not simply categorized as “salient” or “stable”; rather, both qualities are ever-present in varying degrees. In other words, salience and stability are both relative conditions (as opposed to absolute), and form two independent continuums (as opposed to a single continuum with stability at one end and salience at the other).⁷

Lerdahl (2001, 315) has written that “stability far outweighs salience in making reductional choices in diatonic tonal contexts.” He later explains that salience becomes increasingly significant structurally as one moves into contexts where strictly tonal grammar is not present. Similarly, the Schenkerian approach usually prioritizes stability and works best when applied to strictly tonal music, whereas Felix Salzer’s ([1952] 1982) approach often accords increased weight to salience and is appropriate for music that is not strictly tonal. However, Lerdahl goes a step further than Salzer and analyzes atonal music. At this extreme of the spectrum, Lerdahl argues that the lack of stability conditions “collapses the distinction between salience and structural importance” (1989, 73).⁸ In music lying between the poles of strict tonality and atonality, the relative weight of salience and stability is more fluid and is constantly open to question. Moreover, salience itself is a more subjective criterion than stability, creating gray areas that defy quantification.⁹

In Pellegrin 2013, I examine a recording by the Thelonious Monk Quartet where both the composition and performance fall outside of the bounds of strictly tonal jazz, having more in common with modal jazz and postbop. In that case I adopt a Salzerian approach, employing a more bottom-up analytical orientation, according decreased weight to pitch stability, and according increased weight to salience.

The Mehldau excerpt examined below is an example of tonal jazz, but occupies a sort of intermediate ground. The composition is tonal and the improvisation upon it consists mostly of “inside” playing, yet the traditional norms of dissonance resolution are stretched or ignored to the point that dissonances themselves become structural. A strict Schenkerian perspective would not consider these dissonances to be structural beyond the lower levels. However, depending on the repertoire at hand, an approach following Lerdahl and Salzer does not require unstable events to always derive their structural weight from the stable events to which they resolve (or could resolve), instead allowing the relative salience of events to become a greater or even principal determinant of structural importance.¹⁰  

My approach to Mehldau’s improvisation is also informed by the Stable Norms and Salient Deviations (SNSD) model I introduce in Pellegrin 2022 (82–85). The model describes how deviations from the underlying form are unstable, but may be salient, creating expressive contrast with the underlying structure. This tension exists within the composition itself, within the performance itself, and between the performance and the composition. In this model, the concept of stability is extended to include rhythm ((hypermetric) downbeats), grouping (phrase structure and cadential closure of the original tune), and the original theme.¹¹

I do not argue that the analytical approach employed in this article is the best or only way to consider Mehldau’s performance, nor that the notions of coherence and unity often prized in the Western art music tradition are necessarily valued by jazz artists in the same way.¹² In addition, while Western methods have often claimed analytical authoritativeness, my approach contributes to the destabilization of this dynamic. First, there is the question of the degree to which salience and stability are valued in a given analysis relative to one another. As mentioned above, this matter can be particularly difficult to resolve in music that is neither strictly tonal nor atonal, as in my work on Robert Glasper (Pellegrin 2022) and Thelonious Monk (Pellegrin 2013) (the latter featuring multiple interpretations), and is also a significant question in the present analysis. Second, my analysis overall places far greater weight on salience, which itself is a more subjective criterion than stability.¹³ It must also be remembered that the recording examined below represents only one of Mehldau’s many performances of “All the Things You Are,” and that transcriptions are subjective documents.¹⁴

As a brief introduction to the subject of common tones, consider their usage in the traditional core theory curriculum vis-à-vis that of introductory jazz improvisation courses.¹⁵ In both contexts, students are taught to use common tones to help them smoothly navigate a given harmonic progression. Also in both contexts, the harmony fluctuates as a tone is repeated (or sustained); a common tone is perceived differently as the harmony changes. However, common tones in traditional part-writing exercises often appear as stable chord tones and are typically found in inner voices, while in jazz they are comparatively more likely to be unstable and may appear prominently in improvised melodic lines.

In the latter case, the implied resolutions of unstable chord tones—as outlined by Steven Strunk (1985) and Steve Larson (1998, 2009)—are frustrated when the tones are repeated.¹⁶ Sometimes a dissonant tone that is repeated may lose its “‘need’ to resolve,” as Strunk first observed with regards to a sustained eleventh in a descending-fifth progression, where it becomes the root of the next chord (1985, 112).¹⁷ Common tones may be extended for dramatic effect, the degree of pitch stability shifting with each new harmony.¹⁸

We now turn to Mehldau’s performance. Example 1 provides the chorus of “All the Things You Are,” by Richard Rodgers and Oscar Hammerstein II, reflecting the key and preferred chord changes of the trio’s performance. Mehldau and his trio (mostly) play the changes a half step higher than the original, which arguably begins in F minor (particularly when the introduction is taken into consideration), but ends in A$$\flat$$ major. This familiar tune is a tonal composition in AABA song form, the second A occurring at a different pitch level, with thirty-six measures overall rather than thirty-two, due to an expansion of the final A section.¹⁹ The audio for Example 1 provides the trio’s performance of the head, to acclimate the reader to the higher key, $$^7_4$$ meter, tempo, and so forth. (Further discussion of the meter and a hypothetical realization of the theme in $$^7_4$$ is given below.) One notable deviation from the original chord changes is the V/$$\flat$$II – $$\flat$$II (F⁷ – BbM7) progression that is consistently played near the end of the form. The theme is performed loosely, and is omitted during this reharmonization (mm. 31­–33), avoiding apparent conflicts between the two.

The A sections of the theme feature 10–7–10–7 linear intervallic patterns composed of strong guide tones—thirds and sevenths—making Mehldau’s relationship with the theme easily perceivable. While he often avoids these thirds and sevenths entirely, he also connects with the theme in ways ranging from subtle reference to direct quotation of several measures at a time (sometimes in the left hand).

Example 2 provides a hypothetical realization of the theme in $$^7_4$$ during measures 212–237, for comparison with the solo excerpt from these measures that is analyzed below. One measure of $$^7_4$$ is equivalent to two measures of the original tune. The eighth-note subdivision of the meter is 4+4+3+3.

Example 3 gives a transcription of the fourth chorus of Mehldau’s main improvisation on “All the Things You Are,” which occurs fairly early on in his twelve-chorus solo. Chord symbols reflect the changes generally played by the trio. The underlying 4+4+3+3 subdivision has been beamed as 4+4+6—despite the fact that other groupings are sometimes projected—for three reasons: 1) ease of visually perceiving the meter (though unusual tied figures do at times result); 2) Mehldau generally projects 6 in this chorus, leaving the 3+3 to be articulated by bassist Larry Grenadier; and 3) to maintain a neutral notation style, thereby avoiding circularity between the processes of transcription and analysis, both of which are interpretive.²⁰ 

Example 4 provides a reduction of the upper voice of Mehldau’s right-hand line, based upon salience. Roots are provided on the lower staff. Dissonances are indicated between the staves. Slurs are only used to connect pitches that are the same, in order to delineate the plateau-like boundaries within which linear motion occurs. Theme tones have been labeled “TT.” Middleground common tones can be seen wherever multiple notes on the lower staff apply to a single note on the upper staff. Note the neighbor motions, and the octave displacements in the last A section.

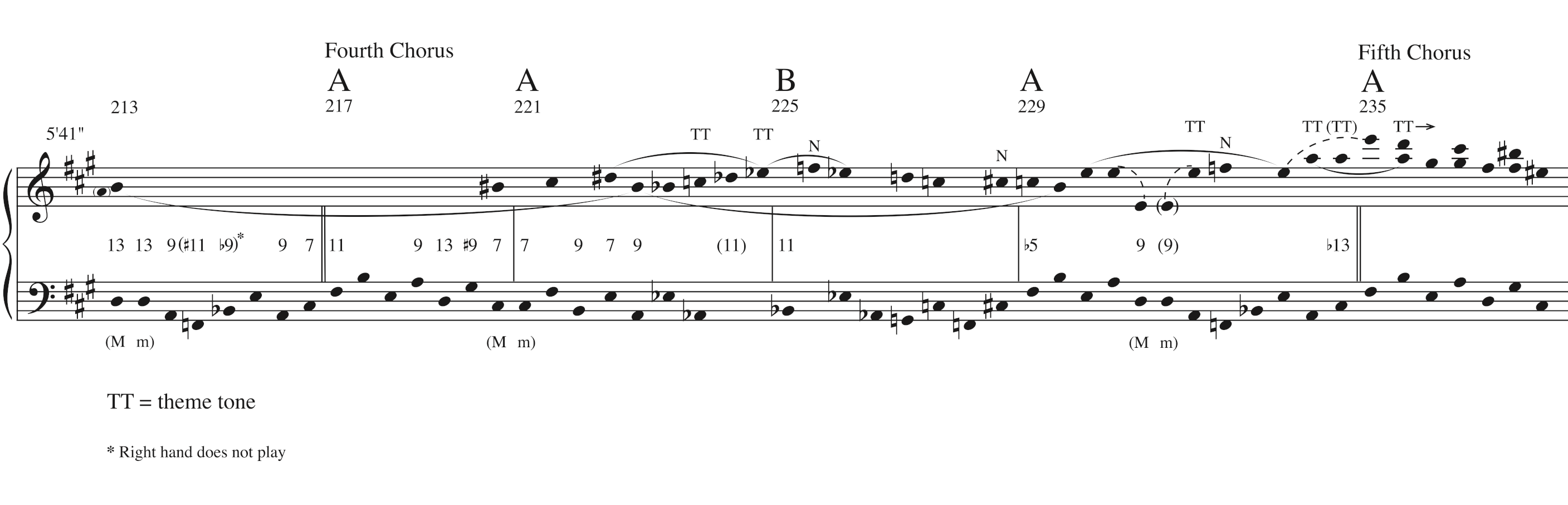
For the first seven measures of the passage, Mehldau confines his right hand to the notes E, A, and B. Initially, A appears to be the structural tone, with B functioning as an upper neighbor. A is a stable chord tone in measures 213–214, and has some salience due to duration and metric placement. B has a similar degree of salience due to register (it is the highest tone) and loudness (which is not reflected in the transcription but may be heard in the audio).

However, it soon becomes clear that the trichord {E, A, B} is superimposed wholesale over the chord changes. The stability of the constituent tones thus fluctuates as the harmony moves through descending-fifth progressions, with each tone appearing in turn as lower chord tone, extension, and alteration. But Mehldau’s playing in the excerpt overall depends less upon chord-tone functionality than upon middleground-level linear motion created by the salient tones, regardless of their harmonic status within the chord or progression. And, during these first seven measures in particular, the stability conditions of Mehldau’s melodic line become almost completely nullified, with salience conditions necessarily stepping in to fill the analytical void. This negation of stability is confirmed by Mehldau’s obvious departure from the chord changes in his left-hand voicings during measures 218 and 219—starting right at the arrival of the stable harmony AM7.²¹      

While he continues to work with these three tones, the B takes on much greater salience as its durations increase and Mehldau begins to repeat the B before moving on to the next pitch. B also continues to be played louder and is still the highest tone. By the time the upper voice moves to B# in measure 220, B has clearly been established as the structural tone, and a linear connection is heard between B and B$$\sharp$$.

This B$$\sharp$$ in measure 220 is the seventh of the C$$\sharp$$-major chord that is the harmonic goal of the first A section. When the harmony changes to C$$\sharp$$ minor at the beginning of the second A section, Mehldau keeps the upper voice on B$$\sharp$$. The major seventh is often played on a tonic minor chord, but not so often on these opening A section harmonies, which also function as submediants in their relative major keys; in addition, not changing the quality of the seventh in this case has the effect of diminishing the distinction between the two chords. However, Mehldau is more concerned here with line and directionality than with clearly projecting each harmony in the form. The line continues to rise, via a fifth (C$$\sharp$$ over F$$\sharp$$), ninth (C$$\sharp$$ over B), and seventh (D$$\sharp$$ over E), before returning back to the B, which appears as a ninth (B over A).²²  

The rising line, including the B with which it begins, thus consists mostly of dissonances that do not resolve tonally—at least not directly. Some of the dissonances could potentially be explained with Schenker’s concept of reaching-over, as shown in Example 5. The B$$\sharp$$ in measure 221 could be heard as resolving (by augmented second) to the A later in that measure, while the C$$\sharp$$ in measure 222 resolves to the B later in that measure. However, resolution tones are not available for the D$$\sharp$$ in measure 222 and the B in measure 223. One could claim an implied soprano C$$\sharp$$ on the A-major harmony in measure 223, providing a resolution tone for the D# as well as demoting the B to the alto voice, where its lack of resolution would presumably be less problematic.²³

However, implying tones simply because they are needed to make an analysis “work” is an abuse of the technique; the mere fact that the analysis can be “solved” on paper using strict techniques does not make it convincing. Those opposed to Salzerian approaches object that anything can be argued with salience, no matter how unconvincing, due to its subjectivity. But this implied-tone analysis offers a reminder that anything can also be argued with strict Schenkerian, approaches by abusing or overusing the otherwise valid techniques of implied tones, cover tones, substitution, and so forth. “Correct” but unconvincing analyses can be produced in either tradition. (Choosing the right tool to begin with will help regardless. The mere presence of tonal grammar in the underlying chord changes does not automatically mean that a strict Schenkerian approach is called for, as anything can be superimposed over a set of chord changes, including random pitches and rhythms.)²⁴

In addition, the reaching-over analysis itself is somewhat unconvincing—and certainly insufficient—as an explanation of the passage. The A, located in the middle of an arpeggio, is completely overpowered by the C$$\sharp$$s, which are accented phenomenally—with loudness, duration, and repetition—as well as metrically, due to the placement of the last C$$\sharp$$ on the downbeat of measure 222 (Lerdahl and Jackendoff 1983, 17). The B in measure 222 occurs in the middle of a rapid scale in which the only tone accented phenomenally (with loudness) is the local- and regional-level apex tone D$$\sharp$$. There is no metrical accent on the B either, as the bass walks in seven during these measures, nullifying the 3+3 subdivision.

Within the context of the repertoire typically studied with Schenkerian analysis, this lack of salience would be more tenable, because of the weight given to pitch stability and tonal resolution in the music itself. After all, one of the fundamental arguments of Schenkerian theory is that salience does not necessarily correspond with structural significance. But salience still plays an important role in analyzing this repertoire, it is just that stability “far outweighs salience,” as Lerdahl stated in the quotation above (2001, 315; emphasis added). Again, this is consistent with the writings of Schachter and Rothstein.

In the present context, our perception of what is stable has to compete much harder with our perception of what is salient. We do hear dissonances in terms of their implied resolutions, owing to the force of the piece’s descending-fifths harmonic scheme, but it becomes increasingly difficult to do so as the dissonances pile up and the resolutions become fewer and further between.    

More importantly, these salient dissonances create their own local and large-scale structures, as can be seen in the reduction. On a local level, there is the rising line that began with B$$\natural$$ and concluded with D$$\sharp$$ (followed by the return to B in m. 223). During the next six measures, these endpoints B and D$$\sharp$$ (occurring later as E$$\flat$$) continue to define the limits between which stepwise motion occurs—forming a sort of channel—until the E$$\flat$$ upper limit dramatically gives way to E$$\natural$$, preparing a quotation of the theme.

Continuing on with the local-level analysis, measures 224–229 feature triadic structures and stable middleground pitches. However, these triads do not always correspond to the underlying harmony, and salience still plays a significant role here.²⁵ Example 6 shows the triadic voice leading of measures 224–229. There are four triads, marked by asterisks, that do not correspond with the chord changes occurring at the time. The first of these, the B$$\flat$$-minor triad in measure 224, is significant in that it initiates the planing passage, but simply functions as a diatonic passing chord. (The 11 marked in Example 4 here is in parentheses to indicate the passing function of this triad.) When the triad occurs again in measure 225, it has a neighboring function, though the chord change here itself is B$$\flat$$ minor. This is because measures 224–226 (and half of measure 223) are all in A$$\flat$$ major, by far the longest segment of the form where a single key is projected. Mehldau takes advantage of this opportunity to plateau on E$$\flat$$—a tone common to the I and V chords, and previously heard as D$$\sharp$$—establishing it as the goal of the rising middleground motion, but briefly pushing up to F to address the pre-dominant harmony.

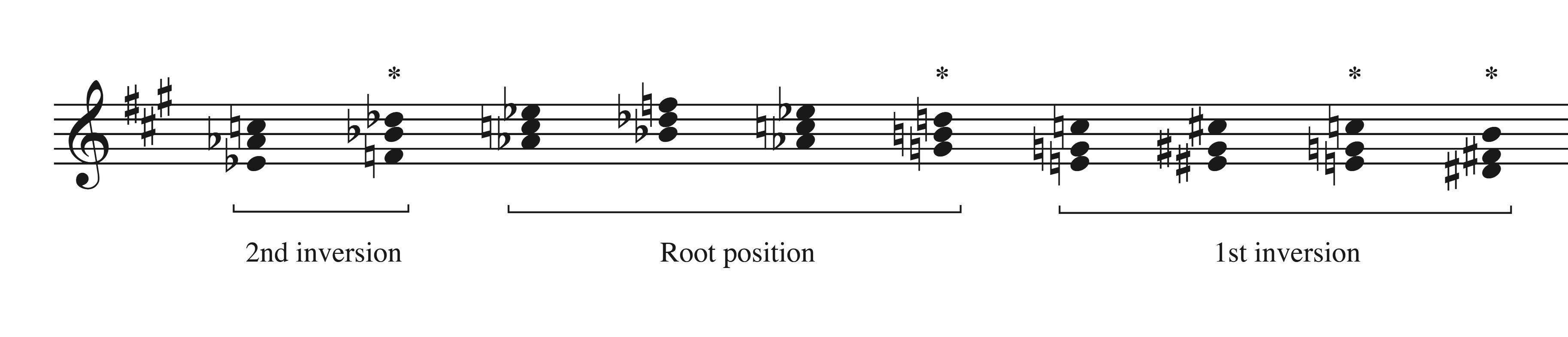
The second asterisked triad is the G-major chord outlined in measure 227. The original chord change is minor rather than major in quality, and some lead sheets indicate a half-diminished quality instead.²⁶ In his left hand, Mehldau substitutes a dominant voicing for the minor harmony, a common technique (particularly in descending fifths progressions) that partly explains the major triad in the right hand. But this G-major triad also initiates a stepwise descent that consists entirely of major triads. (A brief neighbor motion up to C$$\sharp$$ echoes the previous motion to F.) In measure 228 Mehldau arpeggiates a C$$\sharp$$ dominant chord—briefly adding a seventh to the triadic planing structure—but then chooses not to resolve it to F$$\sharp$$ harmony given in the changes. This tonic F$$\sharp$$-minor harmony is significant as it marks the return of the A section, and accounts for the unusual harmonic motion from F major to C$$\sharp$$ dominant. However, Mehldau plays a C-major triad instead, continuing the linear descent chromatically. The goal of this descent is B, the lower plane he initially established, and reinforced in measure 223.   

In focusing on triads built from roots, Mehldau avoids sevenths during these measures (except for the C$$\sharp$$ chord). In the upper voice, shown on the reduction, he avoids thirds as well, emphasizing roots and fifths. (Note the middleground parallel fifths that result in mm. 226–227.) This may be because the theme of “All the Things You Are” consists mostly of thirds and sevenths—accentuating these chord tones would thus reference the theme, a technique which is saved for other occasions.²⁷ The texture that results from planing triads in this way has a stable and open quality most of the time, but differs from the guide-tone flow characteristic of traditional bebop lines, which tends to feature stronger resolutions. With the sevenths omitted and some chord changes dominantized (changed into dominants) or ignored altogether, the ear focuses more on linear directionality, including the parallel up-down-down contours engendered by the neighbor motions, than on the underlying tonal logic.

As can be seen in the transcription (Example 3), the endpoint of the stepwise descent, B, is reached in measure 229 via a B-major triad, the last of the four anomalous chords shown in Example 6. The original changes are further obscured when Mehldau curiously seems to resolve this chord as if playing a V7–I progression in E major.²⁸ The octave-long E major scale that follows pushes a half-step higher than the previous E$$\flat$$ plateau, connects E₄ with E₅ to create a powerful octave articulation of this pitch class, and furthers the sense of E major through the use of D$$\sharp$$ rather than D$$\natural$$.²⁹ Mehldau continues to work within the compass of an octave, firmly establishing the new common-tone plateau of E.

The beginning of measure 231 provides valuable insight into Mehldau’s priorities regarding stability and salience in this passage. He could easily have continued the descending scale at the end of measure 230 to arrive at F$$\sharp$$ on the downbeat of measure 231, the third of the chord, reconnecting with the original changes (and theme). However, he instead skips over the F$$\sharp$$ to arrive at E, the ninth of the chord. This tone is not stable, but is salient, due to its metric placement, duration, articulation, the skip in the line that precedes it, the rests that follow, its position as a valley tone in the local contour, and the parallelism created by its proximity to other salient Es (particularly the downbeat of measure 232). Moreover, this ninth does not resolve, but rather is carried over into the next measure, losing its “‘need’ to resolve” (Strunk 1985, 112). These observations demonstrate that here Mehldau is concerned more with projecting a middleground plateau of E than with attending to the tonal resolutions implied by the chord changes.³⁰ 

Many of the parameters I mention in the paragraph above in support of the salience of E₄ may be found in Lerdahl’s list of salience conditions (1989, 74; 2001, 320). However, it must be understood that this list, while convenient, only pertains to certain aspects of Lerdahl’s theory, and does not comprehensively entail his concept of salience. As one example, the principle of change does not appear on this list, but applies to many of the items on the list: a change in one of the conditions itself creates salience (as mentioned above). Lerdahl and Jackendoff discuss this principle of change in their explanation of Grouping Preference Rule 3, Change (1983, 45–49; see also Schachter 1976, 40–41).

Of the reasons I gave why the E on the downbeat of measure 231 is salient, metric placement, duration, and parallelism (discussed below) are on Lerdahl’s list of salience conditions. Articulation is not on this list—probably because it is a combination of loudness and timbre, both of which are on the list. Several of the reasons I gave relate to the principle of change. I mentioned “its position as a valley tone in the local contour,” an application of the change principle to melodic direction. I mentioned “the skip in the line that precedes it.” Lerdahl and Jackendoff consider leaps of any size as a change of register, which they measure in terms of “intervallic distance,” and any leap occurring singly within a context of stepwise motion will increase the salience of the note following the leap, as in the examples they discuss (1983, 46–47).

I mentioned “the rests that follow.” In the language of Lerdahl and Jackendoff, the rests in measure 231 form a “discontinuity” with the notes that follow, as does the “relatively greater interval of time between attack points.” Both of these factors create a “distinctive transition” after the E, “that intuition will favor as [a] group [boundary]” (1983, 44). This comes from the authors’ discussion of Grouping Preference Rule 2, Proximity, the parameters of which also do not appear on the list of salience conditions.

I mentioned “the parallelism created by its proximity to other salient Es (particularly the downbeat of measure 232).” Parallelism is given on the list (“parallel to a choice made elsewhere in the analysis”), but the subject is complex. Lerdahl and Jackendoff give more detail on pages 51–53, where they state: “among the factors involved in parallelism are similarity of rhythm, similarity of internal grouping, and similarity of pitch contour.” Rhythm and pitch contour are both relevant here. The E in measure 231 fits into a pattern of Es occurring in the surrounding measures that are both metrically accented and constitute peak or valley tones—this occurs twice in measure 230 (E₄ and E₅), and in measures 232 and 233.

During measures 230–233, four scales beginning in the second half of each measure exhibit nested antecedent-consequent relationships resembling those of parallel double-period structure (see Example 7). The descending scale in measure 230, leading down to E (with the skip), is answered, though inconclusively, by the ascending scale at the end of measure 231, which leads up to E. (This descending-ascending scalar motion itself references that of measures 222–224.) Another antecedent-consequent pair of scales then answers the first pair. In measure 232 the upper voice E moves up to F to address the Neapolitan area. (The octave-space E₄–E₅ is also shifted up to F₄–F₅.) The scale descending from E at the end of measure 233 is outstandingly skillful. In this one motion, Mehldau 1) answers the descending scale at the end of measure 232 with exact intervals, exploiting the half-step motion created by the $$\flat$$II substitution changes (F7 to E7) in a sort of sideslip gesture; 2) returns to E, thus defining F as a neighbor tone to the E plateau and paralleling the F neighbor tone from measure 225; 3) echoes the first of these four scales (occurring in measure 230), now replacing D$$\sharp$$ with D$$\natural$$ to project A major (rather than E major) just in time for the final cadence of the chorus; and 4) realigns the E plateau with stability, E now being the root of the chord (as it was when the plateau began).

While this descending scale from E₅ functions as a consequent to the others, it also forms part of a new antecedent. This antecedent and its consequent both follow the same order of events: an onbeat eighth rest, a step or leap up to a foreground-level apex tone with middleground-level structural significance, a descending scale, a sudden reversal of direction, and an upwards motion through an octave that pushes the line to new highs. The overall motion is from E₅ up to A₅, and then from A₅ up to E₆, establishing A as a structural tone and completing the register transfer shown in the reduction. (Curiously, this new antecedent, except for the rest, is also an exact transposition of a segment of measures 229–230, though with different metric and harmonic relationships.)³¹

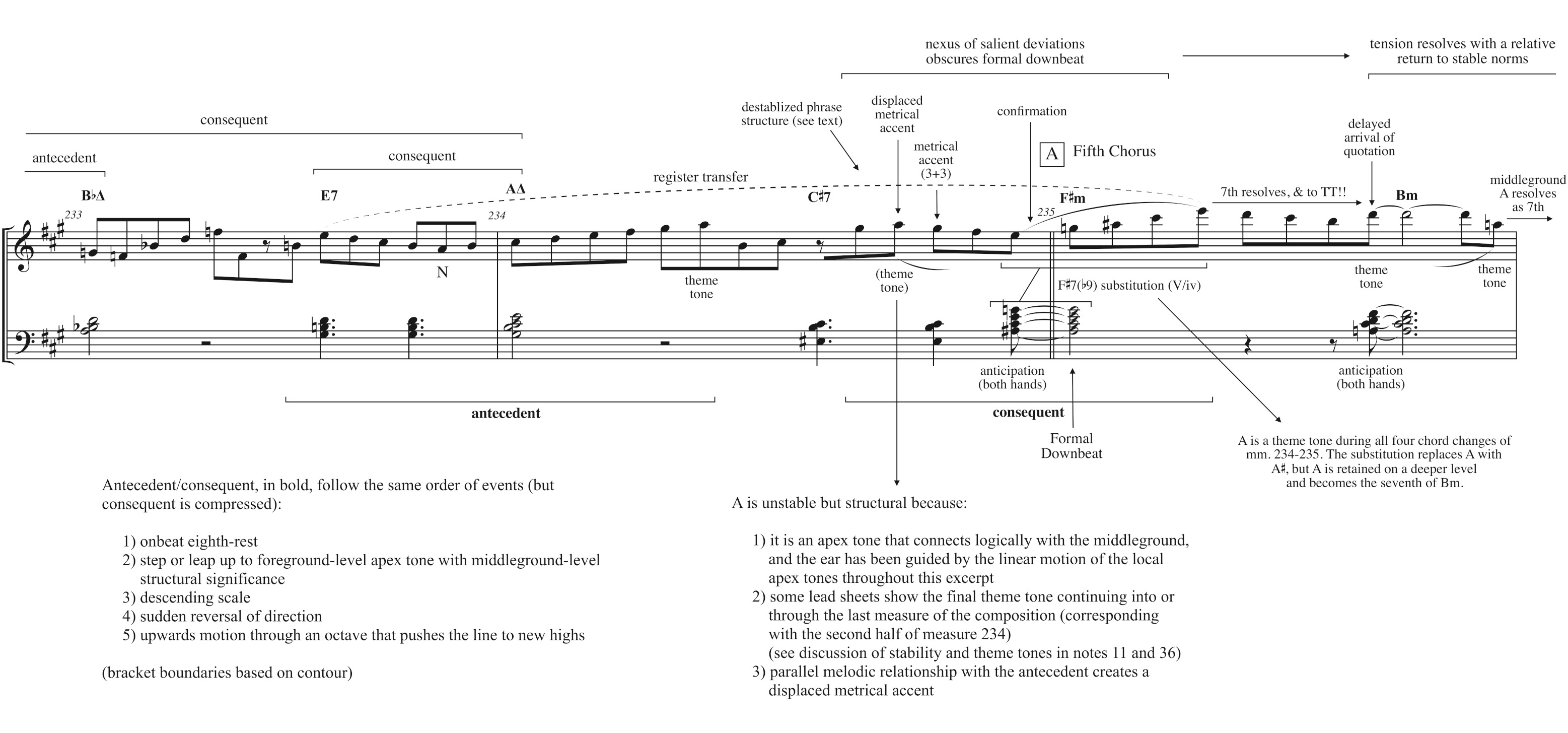
The consequent traverses the events outlined above in compressed fashion, intensifying the dramatic effect of the moments before the theme is quoted. Specifically, the consequent occurs one quarter-note later in the measure, has a shorter descending scale, and skips rather than steps up through the octave. Example 8 provides a detailed view of measures 233–235, and is beamed 4+4+3+3.³²

Recall that E5 had been the structural tone for four complete measures (230–233), interrupted only by the neighbor motion to F (the highest tone in the excerpt up to this point). The overall upwards motion of an octave (E₅–A₅–A₅–E₆) effected by this final antecedent/consequent pair is itself therefore quite significant, but the final approach to E₆ is especially striking. The descending scale of the consequent retraces the upwards middleground motion from the A back down to E₅, upon which an arpeggio is built that launches the line up to E₆. This foreground-level arpeggio from E₅ up to E₆ might be considered a hidden repetition of the middleground-level register transfer. In this case, the arpeggio would be what Larson refers to as a “confirmation,” since it “simultaneously completes its path and the path of the larger model it represents” (2008, 252).

With this arpeggio, Mehldau again substitutes a dominant (F$$\sharp$$7($$\flat$$9)) for a minor chord, the seventh of which resolves down to the theme tone D, initiating a passage of direct thematic quotation. His arrival at this point is clear but does not sound predictable—the dominant substitution occurs at the beginning of the new chorus, which has the effect of 1) delaying the arrival of the quotation until the second chord and theme tone, 2) tonicizing B rather than F$$\sharp$$, and 3) extending the phrasing of the eighth-note line over the chorus boundary.³³ This phrasing differs from the phrasing earlier in the excerpt, which was far more normative. For example, Mehldau frequently concludes phrases on or near downbeats, which represent two-bar hypermetric downbeats in the original tune. See especially measures 222, 223, 224, 226, 231, and 232. During the nested antecedent/consequent pairs (measures 230–233), the apex tones also agree with the metric and harmonic structure, but this stability breaks down entirely in measure 234.

It should be observed that A is a theme tone during all four chord changes of measures 234–235. (A is both the first and last note of the theme.) Mehldau references this theme tone A in measure 234, and returns to it at the end of measure 235. Dominantizing the F$$\sharp$$ chord briefly replaces A with A$$\sharp$$, though on a deeper level the A is retained, as shown in the reduction. Part of the effectiveness of this passage derives from hearing the E and A, which have been clearly established as structural tones, become the sevenths of the F$$\sharp$$ and B chords, despite the disruption of the A$$\sharp$$, and then resolve downwards by step—the first time in this excerpt that middleground dissonances have resolved in such fashion.³⁴³⁵

The second half of measure 234 is quite complex and requires further explanation. The A is not stable, and left-hand chords again delineate 3+3 here, placing the chord tone G$$\sharp$$ on a beat. However, the A is perceived as structural because 1) it is an apex tone that connects logically with the middleground, and the ear has been guided by the linear motion of the local apex tones throughout this excerpt; 2) some lead sheets show the final theme tone continuing into or through the last measure of the composition (corresponding with the second half of measure 234), indicating that this A, like those that immediately precede and follow it, is thematic; and 3) the antecedent/consequent relationship discussed above entails parallelism, a form of salience; thus, we hear the A as structural (despite its instability) because we heard the E in measure 233 as structural. The parallel melodic relationship with the antecedent also creates a displaced metrical accent on the A that conflicts with the metrical accent on the G$$\sharp$$, producing, in conjunction with the anticipation of measure 235 in both hands, a complex rhythmic moment.

Taken together, the anticipations in both hands, metric displacement (including the conflict between the right hand and left hand), F$$\sharp$$7($$\flat$$9) substitution, and phrase structure form a nexus of salient deviations that obscures the formal downbeat and other aspects of the underlying form (Pellegrin 2022, 82–85).³⁶ This tension with stable norms then resolves substantially as Mehldau returns to the original theme (though syncopated), which he had paraphrased during the first two choruses.

In addition, Example 8 may be compared fruitfully with the Robert Glasper analysis shown in Figure 20 of Pellegrin 2022 (97), as well as with the Bill Evans analysis found in Pellegrin 2016. In all three cases, there is a dramatic buildup of salient deviations leading into the succeeding chorus, providing some evidence that formal downbeats and their environs are a natural locus of activity.   

In this excerpt we have seen that large-scale structure is created via salience more than stability. Most (though not all) of the notes agree with the harmony, but the line generally does not derive from the resolution tendencies of its constituent chord tones. Mehldau uses middleground common tones (often dissonant) both to establish boundaries (in the form of plateaus) and to move linearly within them. The repeated, arpeggiated trichord {E, A, B} at the beginning of the excerpt is reflected in the E and B plateaus and the later focus on A, which then prepare the return to stability. These factors create a compelling large-scale trajectory for the chorus overall, though this fourth of twelve choruses is itself only a glimpse of the high peaks of energy and complexity occurring in later choruses.

---

References

Arthurs, Daniel. 2011. “Reconstructing Tonal Principles in the Music of Brad Mehldau.” PhD diss., Indiana University.

Boyle, Antares. 2021. “Flexible Ostinati, Groove, and Formal Process in Craig Taborn’s Avenging Angel.” Music Theory Online 27 (2).

Forte, Allen. 1995. The American Popular Ballad of the Golden Era: 1924-1950. Princeton, New Jersey: Princeton University Press.

Jairazbhoy, Nazir. 1977. “The ‘Objective’ and Subjective View in Music Transcription.” Ethnomusicology 22 (2): 263–273.

Levine, Mark. 1995. The Jazz Theory Book. Petaluma, California: Sher Music.

Heyer, David J. 2012. “Applying Schenkerian Analysis to Mainstream Jazz: A Justification for an Orthodox Approach. Music Theory Online 18 (3).

Larson, Steve. 1998. “Schenkerian Analysis of Modern Jazz: Questions about Method.” Music Theory Spectrum 20 (2): 209–241.

———. 1999a. Review of The American Popular Ballad of the Golden Era, 1924–1950 by Allen Forte, The Music of Gershwin by Steven E. Gilbert, and Charlie Parker and Thematic Improvisation by Henry Martin. Music Theory Spectrum 21 (1): 110–121.

———. 1999b. “Swing and Motive in Three Performances by Oscar Peterson.” Journal of Music Theory 43 (2): 283–314.

———. 2008. “Composition versus Improvisation?” Journal of Music Theory 49 (2): 241–275.

———. 2009. Analyzing Jazz: A Schenkerian Approach. Harmonologia: Studies in Music Theory 15. Hillsdale, New York: Pendragon.

Lerdahl, Fred. 1987. “Timbral Hierarchies.” Contemporary Music Review 2 (1): 135–160.

———. 1989. “Atonal Prolongational Structure.” Contemporary Music Review 4 (1): 65–87.

———. 2001. Tonal Pitch Space. New York: Oxford University Press.

Lerdahl, Fred, and Ray Jackendoff. 1977. “Toward a Formal Theory of Music.” Journal of Music Theory 21 (1): 111–171.

———. 1983. A Generative Theory of Tonal Music. Cambridge, Massachusetts: The MIT Press.

———. 1983/1984. “An Overview of Hierarchical Structure in Music.” Music Perception 1 (2): 229–252.

Martin, Henry. 1996. Charlie Parker and Thematic Improvisation. Studies in Jazz 24. Institute of Jazz Studies, Rutgers—The State University of New Jersey / Lanham, Maryland: Scarecrow Press.

———. 2011a. “More Than Just Guide Tones: Steve Larson’s Analyzing Jazz—A Schenkerian Approach.” Journal of Jazz Studies 7 (1): 121–144.

———. 2011b. “Schenker and the Tonal Jazz Repertory.” Dutch Journal of Music Theory 16 (1): 1–20.

———. 2012. “Charlie Parker and ‘Honeysuckle Rose’: Voice Leading, Formula, and Motive.” Music Theory Online 18 (3).

———. 2012–2013. “Expanding Jazz Tonality: The Compositions of John Coltrane.” Theory and Practice 37/38: 185–219.

———. 2018. “Prolongation and Its Limits: The Compositions of Wayne Shorter.” Music Theory Spectrum 40 (1): 84–105.

McFarland, Mark. 2012a. “Bill Evans and the Limits of Schenkerian Analysis.” Journal of Schenkerian Studies 6: 33–66.

———. 2012b. “Schenker and the Tonal Jazz Repertory: A Response to Martin.” Music Theory Online 18 (3).

McGowan, James. 2008. “‘Consonance’ in Tonal Jazz: A Critical Survey of its Semantic History.” Jazz Perspectives 2 (1): 69–102.

Pellegrin, Rich. 2013. “On Jazz Analysis: Schenker, Salzer, and Salience.” PhD diss., University of Washington.

———. 2016. ​“Schenkerian versus Salzerian Analysis of Jazz.” In Form and Process in Music, 1300-2014: An Analytic Sampler, edited by Jack Boss, Heather Holmquest, Russell ​Knight, Inés Thiebaut, and Brent Yorgason, 255–274. Newcastle upon Tyne: Cambridge Scholars Publishing.

———. 2022. “Harmony versus Voicing: Modeling Local-Level Salience and Stability in Jazz after 1960.” Zeitschrift der Gesellschaft für Musiktheorie 19 (1): 67–102.

Rothgeb, John. 1997. “Salient Features.” In Music Theory in Concept and Practice, edited by James Baker, David Beach, and Jonathan Bernard, 181–196. Eastman Studies in Music 8. Rochester, New York: University of Rochester Press.

Rothstein, William. 1981. “Rhythm and the Theory of Structural Levels.” PhD diss., Yale University.

———. 1989. Phrase Rhythm in Tonal Music. New York: Schirmer.

———. 1990. “Rhythmic Displacement and Rhythmic Normalization.” In Trends in Schenkerian Research, edited by Allen Cadwallader, 87–114. New York: Schirmer.

Rusch, René, Chris Stover, and Keith Salley. 2016. “Capturing the Ineffable: Three Transcriptions of a Jazz Solo by Sonny Rollins.” Music Theory Online 22 (3).

Salzer, Felix. [1952] 1982. Structural Hearing: Tonal Coherence in Music. Two volumes bound as one. New York: Dover. Originally published by Charles Boni.

Schachter, Carl E. [1976] 1999. “A Preliminary Study.” In Unfoldings: Essays in Schenkerian Theory and Analysis, edited by Joseph N. Straus, 17–53. New York: Oxford University Press. Originally published as “Rhythm and Linear Analysis: A Preliminary Study” in Music Forum 4: 281–334.

———. [1980] 1999. “Durational Reduction.” In Unfoldings: Essays in Schenkerian Theory and Analysis, edited by Joseph N. Straus, 54–78. New York: Oxford University Press. Originally published as “Rhythm and Linear Analysis: Durational Reduction” in Music Forum 5: 197–232.

———. [1987] 1999. “Aspects of Meter.” In Unfoldings: Essays in Schenkerian Theory and Analysis, edited by Joseph N. Straus, 79–117. New York: Oxford University Press. Originally published as “Rhythm and Linear Analysis: Aspects of Meter” in Music Forum 6 (1): 1–59.

Segall, Christopher. 2020. Prolongational Analysis without Beams and Slurs: A View from Russian Music Theory.” Journal of Schenkerian Studies 12 (1): 183–188.

Strunk, Steven. 1979. “The Harmony of Early Bop: A Layered Approach.” Journal of Jazz Studies 6: 4–53.

———. 1985. “Bebop Melodic Lines: Tonal Characteristics.” Annual Review of Jazz Studies 3: 97–120.

———. 1996. “Linear Intervallic Patterns in Jazz Repertory.” Annual Review of Jazz Studies 8: 63–115.

———. 2016. “Tonal and Transformational Approaches to Chick Corea’s Compositions of the 1960s. Music Theory Spectrum 38 (1): 16–36.

Waters, Keith. 2001–2002. “Outside Forces: ‘Autumn Leaves’ in the 1960s.” Current Musicology 71–73: 276–302.

———. 2016. “Chick Corea and Postbop Harmony.” Music Theory Spectrum 38 (1): 37–57.

1. A version of this essay was presented at the 2016 annual meeting of the Society for Music Theory in Vancouver, BC. I would like to thank the anonymous peer reviewers for their suggestions on the manuscript, as well as Derek J. Myler and David Falterman for their editorial assistance. Art of the Trio, Volume 4 was recorded in New York City, January 5–10, 1999, and released on Warner Brothers (9362-47463-2) with Larry Grenadier playing upright bass and Jorge Rossy on drums. It is also available in the boxed set The Art of the Trio Recordings: 1996–2001; Nonesuch 7559-79839-5.
2. For more on the stability of the form, see Pellegrin 2022, which introduces a jazz listening model called “Stable Norms and Salient Deviations.”
3. See Pellegrin 2013 for a detailed examination of the relationships among these writings (1–42, 108–125). Of these sources, Lerdahl 1989 and 2001 use the specific terms “salience” and “stability” the most extensively. Segall 2020 suggests the term “prolongational analysis” as a replacement for “Schenkerian analysis,” but prolongational analysis is deeply intertwined with rhythmic analysis, as this body of work demonstrates.
4. John Rothgeb’s (1997) analysis of the relationship between stability and salience is entirely consonant with that of Lerdahl and Jackendoff. However, he redefines—at least rhetorically—the notion of salience, ultimately arguing that the structural features of a piece are the truly salient ones. (See Pellegrin 2013, 7–8, for discussion.)
5. A notable exception to this broad classification is Lerdahl 1987, which deals with timbre in hierarchical fashion.
6. This approach to chord tones derives from Larson 1998, which in turn relies upon Strunk 1979, 1985, and 1996. See Pellegrin 2013 (132–142) for discussion. See McGowan 2008 for another perspective.
7. This is not to say that salience and stability do not interact with one another. For examples of such interaction, see Pellegrin 2013, 6–7.
8. In this situation, it could be argued that “salience” does become nearly synonymous with structural “importance,” but only indirectly so, as a result of the absence of stability conditions. Again, neither Lerdahl nor I intend the word “salient” to directly mean “important”; rather, salience is one category of parameters that contributes to decisions regarding structural importance.
9. Readers who are troubled by the subjectivity of decisions based upon salience should refer to the section entitled “Salience and Subjectivity” in Pellegrin 2013 (32–43), as well as to pages 108–25, which discuss Lerdahl 2001. Lerdahl, a theorist of great rigor whose work is in part motivated by a desire to clarify the subjectivities of Schenkerian approaches, ultimately finds that salience is not quantifiable, in contrast with his earlier efforts to demonstrate that it is (as in Lerdahl 1989). Lerdahl (2001, 381) himself writes: “The last three chapters have shown how the entire tonal theory . . . can be applied, with appropriate modifications, to highly chromatic and atonal music. In the process, however, the theory has gradually become less systematic, with increasing reliance on the underspecified interaction of unquantified rules of salience and consonance. Changes in the basic spaces themselves cause this decrease in derivational clarity. If the musical signal does not facilitate the inference and transformation of stratified basic spaces, the listener turns to pyschoacoustic factors to organize the stimulus.”
10. For other modified-Schenkerian approaches to jazz analysis, see Martin 1996, 2011a, 2011b, 2012, 2012–2013, and 2018. For discussion of Martin’s work, see Larson 1999a, Heyer 2012, and McFarland 2012a and 2012b. See also Strunk 2016 and Waters 2016.
11. This characterization of the original theme tones as stable differs from Lerdahl’s definition of stability, as a theme tone may be harmonically unstable. However, Lerdahl does not deal with jazz, and therefore does not need to distinguish between the form underlying a performance and the performance itself. In the SNSD model, original theme tones provide an anchor to the stability of the composition on which the performance is based. In the present article, my language reflects the traditional definition of stability as a function of pitch, as the direct incorporation of the SNSD model was a late addition.
12. Mehldau, it should be observed, is accomplished in both idioms.
13. See note 9, above.
14. Technology does not resolve the issue of subjectivity in transcription. For an introduction to this subject, see Jairazbhoy 1977. For more on transcription issues in general, see Rusch, Stover, and Salley 2016. For more on transcriptions and salience, see Pellegrin 2013, 145–146. The issues mentioned in this paragraph are discussed by Antares Boyle (2021, [2.1.1]–[2.1.6]), who also addresses the preference some jazz musicians have for the term “Black improvisational tradition” and the process-mediated nature of improvisation.
15. For a pedagogical discussion of common tones, see Levine 1995, 155–161.
16. See Arthurs 2011 (45–53) for additional commentary on this aspect of Strunk’s and Larson’s work. Arthurs studies Mehldau’s original music, in contrast to the analysis presented below.
17. Larson 1998 (217) also addresses the question of unresolved dissonances, and McFarland 2012a further examines the issue, focusing on tritone substitution and melodic pedals. McFarland writes, “Melodic pedals can be incorporated into the contrapuntal fabric of a work without exceeding the limits of Schenkerian theory. But this is not always the case” (62).
18. For example, see the Herbie Hancock improvisation discussed in Waters 2001–2002.
19. See Forte 1995 for an analysis of “All the Things You Are.”
20. Mehldau projects other groupings far more often in later choruses. Regarding the third point, it would be unscrupulous to embed my hearing of what is salient into the beaming structure, and then appeal to that beaming structure in my analytical remarks to support an argument for the salience of an event; there are no articulation markings for the same reason.
21. The intervals shown in the reduction at this point are still calculated against the original chord changes for the sake of simplicity.
22. The E at the beginning of measure 223 is stable and is played with more emphasis than the B, but is part of a separate inner-voice line. The B is metrically accented and has a stepwise relationship with the upper line in succeeding measures. (Note the parallel gesture at the beginning of measure 224, where C is in the upper voice.) In the middleground, this return to B is perceived despite the dip down to B$$\flat$$ that follows, which is brief and not particularly salient. The B clearly goes to the C₅ on the downbeat of measure 224, but the B is not active during the E$$\flat$$7 chord. C₄ could be heard as structural during the E$$\flat$$7 chord instead of B$$\flat$$ (by way of register transfer), since C₄ is a valley tone, metrically accented, and phenomenally accented (via loudness) (Lerdahl and Jackendoff 1983, 17). The B$$\flat$$ has a phenomenal accent (as the last note of a crescendo at the end of the measure), and is one of the stable, lower chord tones. Both interpretations are valid.
23. A more clear-cut example of rising lines comprised of salient middleground dissonances may be found in Pellegrin 2016, where I analyze a passage of a Bill Evans improvisation. That essay dealt specifically with rising linear motion comprised of dissonances, whereas the present article is more concerned with common tones.
24. See Pellegrin 2013 (61–68) for discussion of the issues raised in this paragraph, as well as that of “problematic compositions” within the traditional Schenkerian repertoire itself.
25. See Pellegrin 2022 for a detailed study of triadic voicings and Robert Glasper’s usage of them, which is very different from Mehldau’s.
26. I use G minor because that is generally preferred in this performance over G half-diminished.
27. The bridge, from which most of these measures are drawn, features more variety of chord tones than the A sections, but the structural melodic tones are thirds and sevenths (except for the raised fifth in the last measure).
28. On the reduction, the B is shown occurring over the B minor chord, partly for convenience. However, I hear the B-major triad less as a displaced, dominantized B-minor chord than as a result of the planing. Note as well that no left-hand chords, which could offer clarification, are played during these measures.
29. To my ears, the C$$\natural$$ in measure 230 hearkens back to the C-major triad of measure 229. This may be because the C$$\natural$$ of measure 230 and the C₄ of measure 229 are both part of (0136) tetrachords. In addition, both of these tetrachords appear in the context of a four-sharp diatonic collection and comprise tones from that collection, except for the C$$\natural$$ that occurs in each one. The two tetrachords are thus tonally and intervallically identical.
30. In the second half of measure 231, on the beat where the D-minor chord change occurs, Mehldau plays a left-hand voicing with E₄ as the top note. Because of the way this chord is played, and because of the salience of other nearby E₄s, this E₄ almost sounds as if it is part of the right-hand line; in fact, the transcription mentioned above shows an eighth-note E₄ occurring here. It seems, in any case, that the E₄ is mentally retained for the duration of this measure, particularly since there are no other notes occurring during the D-minor harmony that seriously compete with the E in terms of salience. The E is marked parenthetically in the reduction (Example 4) to indicate that it is implied.
31. The two upwards motions through an octave do function differently, as the A₄ in measure 233 is a neighbor tone, not a chord tone. This may seem self-evident, but compare with the segment of exact transposition in measure 229. In measure 229, Mehldau’s playing is more focused on salience, and the E₄ is not a neighbor to F$$\sharp$$, as the B-minor harmony would suggest, but rather is the structural tone, due to the local contours (peak/valley tones). The stability of E as the tonic of the superimposed key is also a factor, though this superimposition is itself a salience-based decision (as well as a large-scale structural one) since it conflicts with the underlying harmony (which is still articulated by the bass). (Recall from above that Mehldau outlines V7-I in E major here, in a sense anticipating the E7 chord, but also ignoring it in favor of an E-major rather than A-major tonality.) Near the end of the chorus the improvisation is increasingly organized around stability, salience thus being less of a factor. Nonetheless, while the A₄ in measure 233 is articulated by a change of direction, the 3+3 division of the 6 is clearly articulated in both hands here, providing both metric and phenomenal accents on B₄ that substantiate the interpretation of A as a neighbor. These left-hand chords articulating 3+3 are in fact E7 voicings, further supporting the neighbor interpretation (as opposed to one considering A₄ as an anticipation).
32. Example 8 is beamed 4+4+3+3 (rather than 4+4+6) because 1) Mehldau articulates the 3+3 in his left-hand chord voicings, 2) the voicings themselves are provided in the example, 3) the metric structure itself is discussed in the analysis, and 4) the analysis is easier to understand with this notation.
33. Mehldau’s choice of E$$\natural$$ at the end of measure 234, as opposed to the E$$\sharp$$ indicated by the changes, can be explained as an anticipation. Examining only his right-hand line, other possible explanations present themselves; however, he plays C$$\sharp$$7 chords in his left hand until the last eighth-note of the measure and then anticipates the F$$\sharp$$ harmony, in conjunction with the right-hand E. In measure 235 it may appear that Mehldau anticipates the B-minor chord starting with the first D he plays, but the comping chords added to Example 8 support the argument that the anticipation occurs with the second D he plays.
34. The flatted fifth (C₅) shown in the reduction at measure 229 occurs as part of the C-major triad that Mehldau plays over the F$$\sharp$$m chord change. This results from planing descending major triads, as discussed above, and is not a case of a chordal dissonance resolving downwards by step.
35. As mentioned in note 11, theme tones may be harmonically unstable, but are considered to be stable in a different sense by the SNSD model, which compares a jazz performance to the compositions on which they are based. In the second half of measure 234, the A₅ is a tone of the original theme (according to some lead sheets), but is also harmonically unstable.
36. Recall that contour, not actual phrase structure, was used to establish the boundaries of the final antecedent and consequent pair. The (sub)phrase itself extends to the half-note D₆.