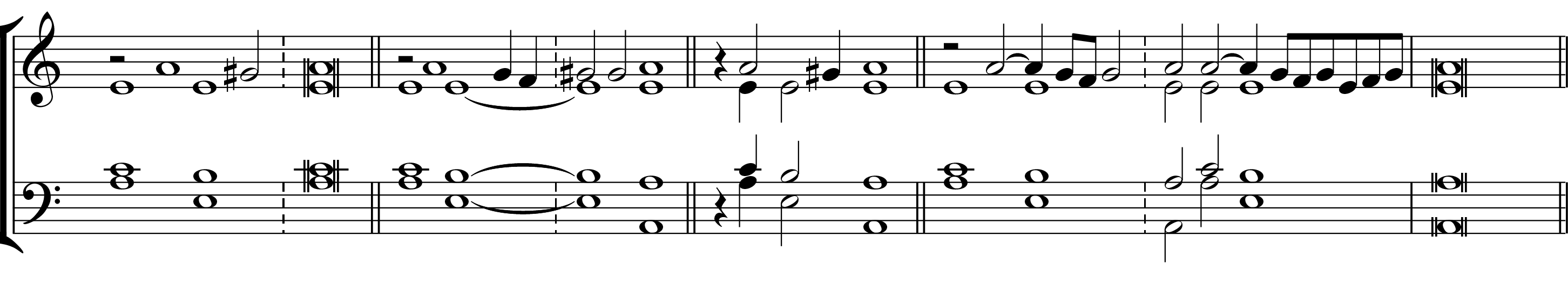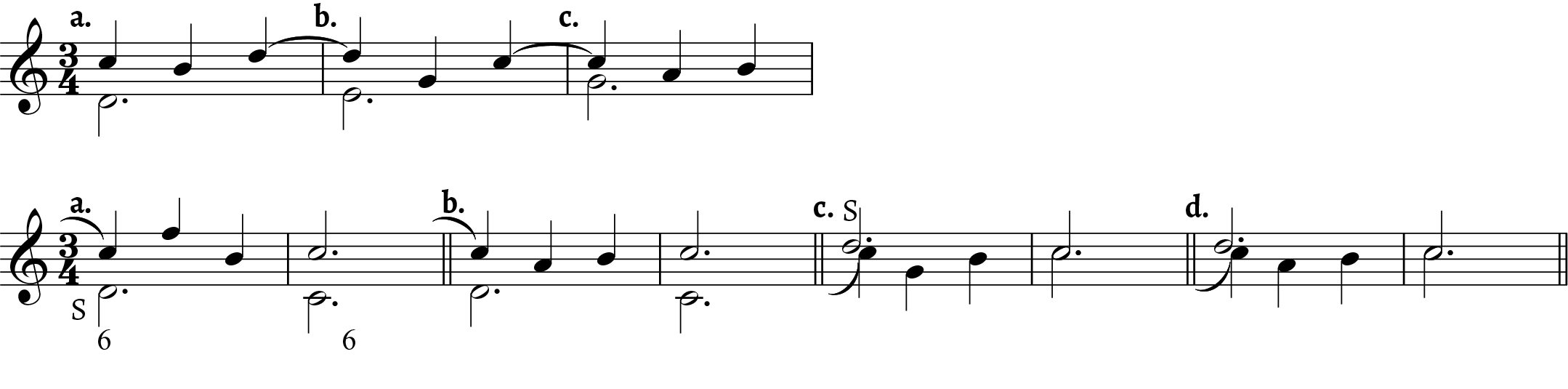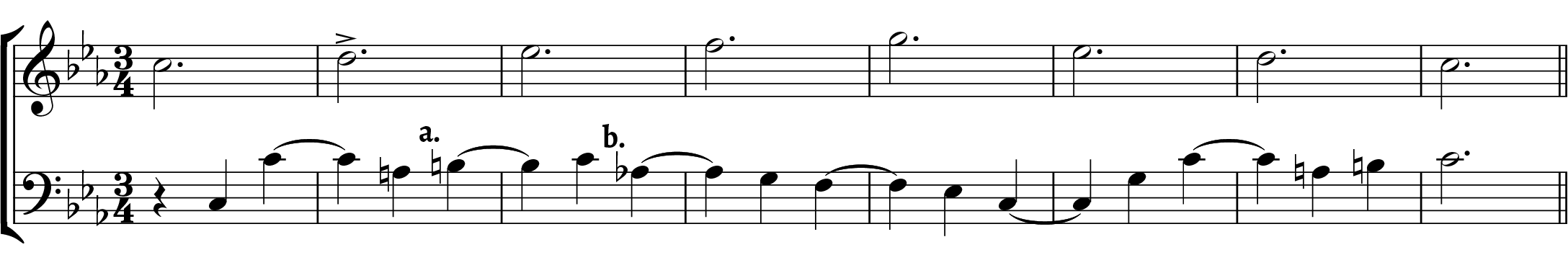Alexander Morgan
Abstract
This article confronts assumptions about how suspensions function and demonstrates how Renaissance suspensions differ from their tonal counterparts. This is primarily due to an additional component in Renaissance suspensions, the perfection phase, which comes immediately after the resolution phase. The difference in the metric structure of Renaissance and tonal suspensions is particularly significant in cases of ternary meter. A corpus study that makes use of the Humdrum Renaissance Dissonance Classifier provides empirical support for the importance of ternary suspensions and their relevance to our understanding of how compositional style changed over the course of the Renaissance. This article also examines dozens of treatises and counterpoint textbooks to highlight some issues with the way that Renaissance suspensions are generally taught and have been taught for centuries.
View PDF
Keywords and phrases: Ternary suspension; perfection phase; dissonance treatment; Johannes Tinctoris; contrapuntal rhythm.
Suggested CitationIntroduction
In this article, I highlight the key points about ternary suspensions to stress how critical they are to a thorough understanding of Renaissance music. After clearly defining “ternary suspensions,” I confirm their prevalence in the repertoire by expanding on a prior corpus study of Renaissance dissonance types.1 The metric placement of Renaissance ternary suspensions is fundamentally different from that of their tonal homologs due to the metric orientation provided by an additional component of Renaissance suspensions, the perfection phase, theorized for the first time here. I demonstrate the main particularities associated with Renaissance ternary suspensions. There are some instances of metric ambiguity in Renaissance music, which compel a discussion of whether a given suspension is heard as binary or ternary. Importantly, ternary suspensions have been largely overlooked in centuries of counterpoint and harmony treatises.2 As Johannes Tinctoris is the most notable exception to this oversight, I revisit his discussion of suspensions to reiterate what he identifies as their primary features. Claudio Monteverdi’s madrigals are highlighted as belonging to a broad transitional period in which compositional practices associated with ternary suspensions began to increasingly reflect tonal standards. Tonal suspensions also garner brief discussion, because knowledge of how Renaissance ternary suspensions function can also influence our hearing of tonal works, as exemplified by an examination of J. S. Bach’s F$$\sharp$$-minor fugue from Book I of the Well-Tempered Clavier.
The dissonance-analysis annotations throughout this paper are all provided by the new Humdrum tool I created with Craig Sapp that is now available on the Josquin Research Project (JRP) website.3 This tool builds on dissonance scholarship by adding detection for some newly theorized types, including distinguishing between binary and ternary suspensions.4 Hereafter, I refer to this dissonance-analysis tool as the “dissonance classifier.”5 Throughout this paper I use Giovanni Maria Artusi’s “patient” and “agent” terminology for describing the components of suspensions in order to clearly differentiate between the contrapuntal functions of different voices in a suspension (Artusi 1598, 47).6 The patient is the suspended note, which I label with an “s” or an “S”, and the agent is the note that moves into the dissonance, labeled with a “g” or a “G”, with lowercase and uppercase characters denoting binary and ternary suspensions respectively. These letters are used instead of “P” and “A” because the dissonance classifier labels forty-four dissonance types and assigns each one a single-character label; naturally, the letters “P” and “A” were already being used for passing tones and anticipations, respectively. In the ternary suspension in Example 1, examined in detail later, the D in the bassus is the agent of a double suspension, with the G and C of the altusand discantus functioning as patients. One must not confuse the term “double suspension” with the unrelated classification of a suspension as binary or ternary. Throughout this paper, I focus exclusively on suspensions, but all other dissonance types that happen to appear in examples are also labeled. For this reason, the reader will also see many of the other labels such as “q”, “c”, and “k” for dissonant third quarters, short-form nota cambiatas, and long-form nota cambiatas, respectively, as well as several others. Each dissonance type is explained with repertoire examples on the documentation page for the analysis tool.7

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color& file=jrp:Obr2018.
1. The Basics of Ternary Suspensions
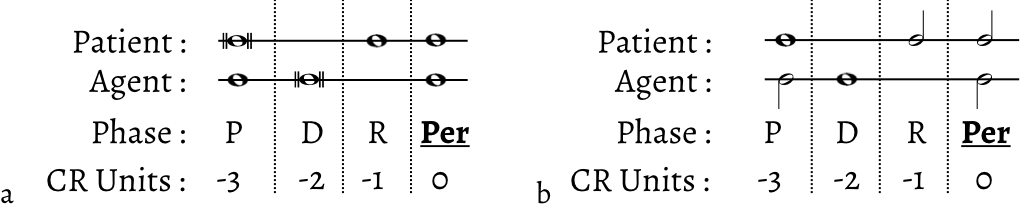
To define ternary suspensions, I draw on the principle of contrapuntal rhythm coined by Ruth DeFord. She describes contrapuntal rhythm as “the rhythm of the structural contrapuntal progressions on which a piece is based” (DeFord 2015, 84). This means that the contrapuntal rhythm of a piece of music is the rate at which new intervals are encountered after reducing out all consonant and dissonant ornamentation.8 This does not mean that all dissonances are reduced out, however, as I consider all the phases of a suspension to be components of the structural counterpoint.9 The first three phases of a suspension—the preparation, dissonance, and resolution—each occupy one unit of time generally equal to the contrapuntal rhythm. If this durational unit groups in threes in the metric organization of the piece, then the suspension is ternary. Example 1 contains a ternary suspension taken from Obrecht’s motet Mille quingentis. This suspension is ternary because the preparation, dissonance, and resolution phases of the suspension each occupy a semibreve (whole note), and semibreves group in threes at this moment in the piece.10 In the agent voice, the note that moves into the dissonance usually lasts twice the duration of the active contrapuntal rhythm, because in unornamented binary and ternary suspensions, it typically spans the dissonance and resolution phases.
The suspension in Example 2 also occurs in the context of a passage notated in triple meter, but unlike Example 1, the preparation, dissonance, and resolution phases (and by extension, the contrapuntal rhythm) operate at the level of the minim (half note), which in turn groups in twos. This means that the contrapuntal rhythm, a minim, is a shorter durational value than the notated beat, a semibreve. In counterpoint treatises and textbooks, the dissonance phase of a suspension is always taken as the phase of reference concerning metric placement. While the dissonance phase of this suspension appears on a weak semibreve, it is strong at the level of the minim, the operant rate of the contrapuntal rhythm. The relative metric weights of the suspension’s first three phases are therefore standard for binary suspensions in that they are relatively weak (preparation), strong (dissonance), and weak (resolution).
Returning to the particularly straightforward suspension in Example 1, its metric profile is completely different from that of Example 2. The former’s preparation is strong and its dissonance weak when we analyze at the metric level of the semibreve, the operative unit of contrapuntal rhythm (hereafter, CR unit). Its dissonance phase is now weaker than the preparation phase. The resolution is still weak, but no longer relatively weaker than the dissonance phase (unless one accords an intermediary strength to beat two of a ternary meter). In Renaissance music, ternary suspensions occur with their dissonance phases in weak metric positions, usually the second unit of a group of three. This is in sharp contrast to tonal music, where the dissonance phase of a ternary suspension almost always occurs on a metrically accented beat. This latter observation is supported by every tonal counterpoint treatise or textbook that covers suspensions in triple meter, such as Walter Spalding’s Tonal Counterpoint (1904, 117–118), which will be discussed later.
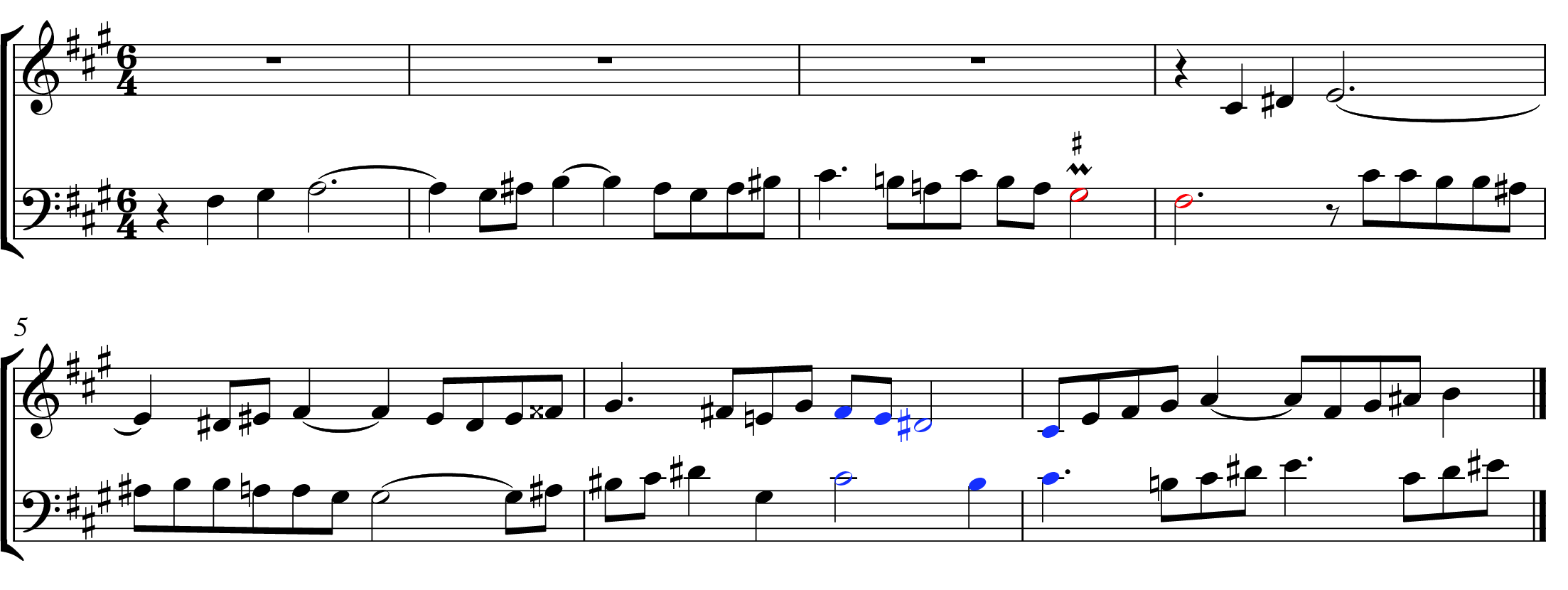
The suspension in Example 3, taken from the same motet by Obrecht, is slightly ornamented. Here the preparation is shortened by a consonant skip from G to E before the dissonance phase. This makes the duration of the preparation phase debatable (a case could be made for either the minim or the semibreve), so it is practical to focus on the durations of the dissonance and resolution phases here to determine the CR unit organizing the structure of the suspension. The dissonance phase of the suspension is also ornamented with a lower neighbor, but the phase’s duration is understood to be unaffected by this ornamentation. The resolution phase is unornamented and lasts a semibreve in duration. In light of the clearly articulated durations of the dissonance and resolution phases, the CR unit of this suspension’s components is the semibreve. As semibreves group in threes at this moment in the piece, this suspension is ternary. This example shows that ornamentation does not materially impact suspension analysis.
Examples 2 and 3 not only come from the same piece by Obrecht, but they also appear in the same passage of the piece, separated by only a single measure, despite their different CR units. Example 4 shows these two excerpts together. The counterpoint between the cadences in mm. 35 and 38 progresses at a noticeably slower rate than in the surrounding measures. The main point to note here is that it is not the mensuration sign, notated time signature, or metric placement (as we will see) that makes a suspension binary or ternary. Rather, the decisive point is how the CR unit groups at the next-highest metric level.

At what point does the CR unit in Example 4 shift? I argue that it happens at the arrival points of the cadences, that is, on the downbeats of mm. 35 and 38. Suspensions are simultaneously the clearest expression of a passage’s contrapuntal rhythm and, when they fully resolve into a cadential perfection, a convincing place to alter the contrapuntal rhythm.
2. Corpus Study
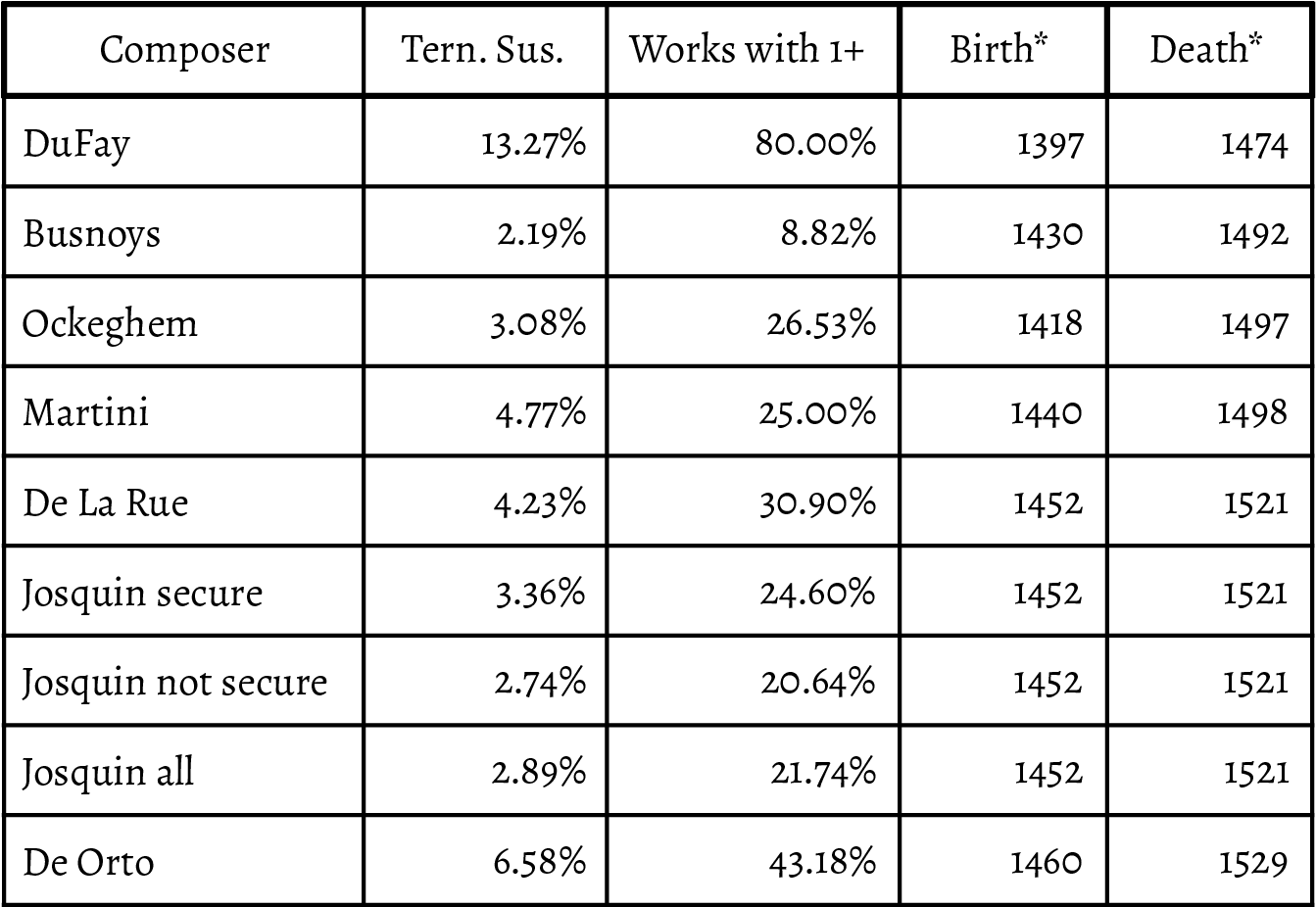
So far, I have only shown examples from a single piece, but examining the data from a corpus study offers a better sense of the prevalence of ternary suspensions. I used the dissonance classifier mentioned above to count the occurrences of forty-four different dissonance types in early- and mid-Renaissance compositions. This identified 158,445 dissonances in a corpus of 1,100 pieces or movements taken from the JRP database. 31,710 of these are labeled as suspensions, of which 1,215 (3.83%) are ternary.11 To put these figures in context, most thorough modal and tonal counterpoint texts include a discussion of “fake suspensions” approached by step.12 This is a contrapuntal scenario where the preparation phase of a suspension is itself dissonant. A query of the same collection of pieces identified just 996 fake suspensions approached by step, meaning that this figure, which garners discussion widely in counterpoint treatises, is actually slightly less common than ternary suspensions, which are rarely ever mentioned. Furthermore, 26.87% of the pieces analyzed feature at least one ternary suspension, thereby cementing the figure’s place as a decisively present, albeit under-examined, feature of this repertoire.
I used the same tool to compare subsets of the repertoire on the JRP database to get an idea of how compositional style varied from composer to composer and changed over time with respect to their use of ternary suspensions. Other studies have used automated dissonance analysis in style-change corpus studies, but this is the only study to distinguish between binary and ternary suspensions.13 I examined the works of seven composers: Guillaume DuFay, Antoine Busnoys, Johannes Ockeghem, Giovanni Battista Martini, Pierre De La Rue, Josquin des Prez, and Marbrianus de Orto. I further break down Josquin’s works into securely and not securely attributed subgroups. For each composer, Table 1 shows the percentage of all suspensions that are ternary, the percentage of pieces examined that have at least one ternary suspension, and each composer’s birth and death years. The chart is organized chronologically by year of death. Though not shown on the chart, there is an obvious connection between a piece’s length and whether or not that piece incorporates at least one ternary suspension: the longer a piece is, the more likely it is to include a ternary suspension. Note that the 20% of DuFay’s works examined that lack ternary suspensions are all extremely short. DuFay stands out as the heaviest user of ternary suspensions, likely due to the high degree of mensural variety in his works. This chart provides but a brief demonstration of what a more complete correlation of dissonance-type usage and style change could reveal. Having established the relative pervasiveness of ternary suspensions in early- and mid-Renaissance compositions, I will now explore how they function in more detail.
3. The Perfection Phase
All treatises and textbooks focus on the dissonance phase as the point of reference for metric placement, which suggests that suspensions are middle-accented. While this is the case for tonal suspensions, both binary and ternary Renaissance suspensions are end-accented because their dissonance phases are not the loci of accentuation. This quality is behind the variety in their metric placement. Ternary suspensions in Renaissance music usually place the dissonance on the weak second beat, but there is some variation in this, and one does occasionally find ternary suspensions with the dissonance on beat one or beat three of a triple group. This variation is due to the fact that in binary and ternary Renaissance suspensions, the metric placement is decided by the fourth phase. Herein lies a crucial point: suspensions in Renaissance music have a fourth phase, which I call the “perfection phase.”
The perfection phase determines the metric placement of binary and ternary suspensions in Renaissance music. As mentioned above, the first three phases of a suspension typically occupy the same durational value, equal to one CR unit. By contrast, the perfection phase often lasts two CR units or even longer. When a suspension successfully realizes its terminal perfection phase, this usually corresponds to some sort of cadence, so the breathing room offered by this comparatively longer phase is appropriate. For the same reason, the perfection phase tends to be metrically strong. The preparation, dissonance, and resolution phases naturally fall, respectively, three, two, and one CR unit(s) before the perfection. This relative distance is the same in both binary and ternary suspensions. Because it is the same in both cases, it is helpful to conceive of this basic durational structure with the metric placement and pitch information abstracted away, as illustrated in Example 5. Examples 5a and 5b represent suspensions with the operant contrapuntal rhythm equal to the semibreve and minim, respectively. At this point, none of the phases should be thought of as strong or weak. Instead, I measure their relative temporal distance in CR units, counting backwards from the perfection phase.
Nicola Vicentino’s (1555) example reproduced in Example 6 shows three durational levels at which one finds suspensions and therefore amounts to a musically contextualized version of Example 5. While Vicentino’s example is helpful, it only includes binary suspensions. Joachim Burmeister offered a very similar example some fifty years later (Example 7), and all of his suspensions are also binary (1606, 114–115, and 117–118; Morgan 2017, 107–108). From these examples we can infer that Renaissance musicians were sensitive to the influence of contrapuntal rhythm on music, even if the concept had not yet been explicitly theorized. The examples indicate that, because of the perfections that end them, suspensions are largely synonymous with cadences.
In a binary suspension, a metrically strong perfection phase places the dissonance on a relatively strong beat as well; in a ternary suspension, on the other hand, the dissonance is relatively weak. This apparent difference is actually incidental, because both situations respect the same distance of two CR units before the metrically referential perfection phase. In Table 2, I contextualize the basic rhythmic structures shown in Example 5 with common effective meters in Renaissance music, but unlike Vicentino and Burmeister, I include examples of both binary and ternary suspensions. The first three phases of each suspension lead to a perfection phase that is metrically strong. To distinguish between binary and ternary suspensions, it is essential to note how the CR unit (which is equal to the basic durational unit of a suspension) groups in the prevailing meter. I show time signatures in these abstract examples instead of mensuration signs because in each case I am asserting a metric hearing, something mensuration signs do not do on their own.

Given the strong metric position and duration of the perfection phase of Renaissance suspensions, this often corresponds to an integral durational value at the level of the tactus (the durational unit into which the CR unit groups).14 In Table 2, each perfection phase aligns with the downbeat, which is the strongest metrical position as well as the most typical position in the repertoire. However, almost all of the time signatures in Table 2 are compound meters, so the perfection phase can fall in more than one relatively strong position. When the CR is equal to the semibreve, the only two truly simple meters are $$2\atop1$$ and $$3\atop1$$ (Table 2a and 2b).15 A mensuration sign or even a time signature alone is not enough information to accurately distinguish between binary and ternary suspensions; one must also know the current CR unit.
Table 2 does not offer an exhaustive list of the contrapuntal contexts in which we find Renaissance suspensions, but it does include the main cases. It demonstrates how the key concepts of perceived metric organization and contrapuntal rhythm set the stage for either binary or ternary suspensions. Examples 1 and 3 include suspensions from Category B. Example 2 belongs to Category C, and in the section of this paper on metric ambiguity, I explore how this relates to the similar-looking Category D. Category C is just like Category E, but in the context of a metric hearing with three as opposed to two imperfect semibreves. Similarly, Category D differs from Category F only in that the former has two perfect semibreves to the latter’s three. There are no Renaissance ternary suspensions in the context of music with a contrapuntal rhythm value shorter than the minim, because all divisions below the minim are binary.
There are, however, many binary suspensions in passages with a contrapuntal rhythm at the semiminim (quarter note), especially from late-sixteenth-century composers such as Thomas Morley. Example 8 shows a binary suspension of this type in mm. 23–24 of Morley’s duet “When Loe by Break of Morning” (1595). There are even suspensions which appear to operate at the fusa (eighth note) level of contrapuntal rhythm. These extremely brief dissonances, however, have no cadential potential, and thus are of a very different nature to all the other Renaissance suspensions considered here. Rather than having the patient move up by step after the resolution phase, these dissonances have no perfection phase. They usually serve to ornament a descent in parallel thirds or sixths with another voice that moves in steady semiminims. Morley makes use of this figure in the first three beats of Example 8. The dissonance classifier assigns such dissonances the label of “o” (for “purely ornamental”), because their fleeting duration and lack of cadential weight make them quite different from real suspensions.

Johannes Tinctoris is well known for being the first music theorist to provide a detailed discussion of dissonance treatment in Book II of his Liber de arte contrapuncti (1477), and his discussion of dissonance treatment is impressively thorough. To this day, no other writer has given as complete an account of ternary suspensions in Renaissance music, a lacuna this article seeks to rectify. In his interval-succession treatise, Tinctoris was systematically restrictive in describing the concatenation possibilities of interval successions that begin on a sixth, thirteenth, or twentieth. Elsewhere, I have shown Tinctoris’s consistent descriptions of these intervals as intermediary consonances (Morgan 2017, 26ff). This is because they were not heard as conclusive sonorities, but rather needed to progress to a perfect interval to conclude a passage.16 David Cohen has traced the philosophical origins of this drive toward intervallic perfection (2001, 142). In so doing, Cohen references Dahlhaus’s summary of a central tenet of contrapuntally conceived music: “one of the basic ideas of contrapuntal theory from the 14th through the 17th centuries is that variation of intervallic quality—the tendency of dissonance toward consonance, or imperfect consonance toward perfect consonance—forms the driving force behind music’s forward motion,” (Dahlhaus 1990, 29). Put another way, throughout the late-medieval period and Renaissance a consonance/dissonance continuum was theorized, and all theorists considered imperfect consonances less consonant than perfect consonances. In light of the relative instability of imperfect consonances as compared to perfect ones, the term “resolution” for the third phase of a suspension is something of a misnomer for Renaissance suspensions, as it is more of an attenuation rather than a complete resolution of the intervallic tension. For example, in cadential suspensions that we would typically label 7–6 or 4–3, the sixth and the third are not the harmonic goals in the intervallic syntax—the perfections that follow them are. For the sake of simplicity, however, I do not recommend changing the term resolution to attenuation, especially as the former allows the third phase of a suspension to be referred to in the same way in both Renaissance and tonal music. Concerning the term “perfection phase,” I chose this name because the harmonic goal of a Renaissance suspension usually results in both harmonic and rhythmic perfection.
4. Special Cases of Metric Placement
There are two basic scenarios wherein the dissonance phase of a ternary suspension does not occur on the second beat of a group of three: either in situations when the perfection phase is relatively weak metrically, or in chains of suspensions. The first, less common situation weakens the cadential arrival, and so is suitable for low-level interior cadences or situations in which a cadence was evaded or abandoned. Example 9 demonstrates this point with a ternary suspension whose dissonance phase is metrically strong. Had this suspension realized its potential for a cadence by progressing to the perfection phase, it would have done so on the metrically weak third semibreve of m. 16 (marked red). The cadential weight of this moment is evaded by the move of the tenor up a step as opposed to down a fifth in the manner of a bassizans cadential-voice function, which one may have reasonably expected.17
A performance or edition of this piece, if it sought to acknowledge this unrealized potential, might add appropriate ficta (that is, raise the first two C’s in m. 16 of the altus). Even on a first hearing, on the basis of its metric placement alone one may suspect that this passage will further erode its rhetorical weight with its intervallic content (by avoiding cadences to perfect intervals). Specifically, beat three of m. 16 can be expected as a probable continuation as early as the downbeat of m. 16. Such an expectation is possible when one knows that the typical metric position of a ternary suspension places the dissonance phase on the second beat of a group of three. This point conveys the importance of being familiar with ternary suspensions in order to have a more active creation of expectation when listening to Renaissance music.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Jos0302b
On the subject of the listener’s expectation in Renaissance music, it is important to note that there are cases of metric ambiguity. In some cases, “metric ambivalence” or “polymeter” may be more accurate terms, as different voices or aspects of a passage may project conflicting rhythmic organizations. Taking m. 15 of Example 9 in isolation, a logical hearing of the altus line—because of its longer notes on the first and fourth minims—might infer a $$6\atop2$$ meter. As I have noted elsewhere, this metric malleability is largely due to the fact that m. 15 has no dissonance in it, and dissonance treatment plays a crucial role in our interpretation of meter (Morgan 2017, 135–136). Measure 16 does include some dissonances, but the neighbor tones and passing tone in m. 16 (labeled “n” and “p”, respectively) are little help because these “non-structural dissonances” operate at the weak semiminim level and therefore do nothing to clarify the minim level of metric organization. Most suspensions are structural dissonances, and the one in m. 16 is no exception; it clearly articulates a $$3\atop1$$ hearing with the dissonance, resolution, and perfection phases of the suspension resolutely falling on the first, second, and third semibreves of the measure, respectively. The turn figures in the superius and altusare common dissonance-phase ornaments for a patient voice (similar ornaments appear in Examples 3 and 4) and have no impact on the beginnings and endpoints of the various suspension phases. Therefore, by m. 16, a $$6\atop2$$ hearing is no longer tenable. I will address how metric ambiguity relates to the analysis of suspensions as binary or ternary shortly.
Example 10 is a clear binary-suspension version of a situation where the perfection phase does not coincide with the onset of an integral breve (i.e., the downbeat as notated). Here the superius and contratenor altus from the Sanctus of Busnoys’s Missa L’homme armé form a phrygian cadence to A in m. 44 that arrives at its perfection (marked red) at a point that coincides with a weak semibreve, thereby vitiating the conclusiveness of the cadence.18 We must remember that, while this passage is notated in triple meter, the CR unit is the minim. Thus, this is a binary suspension, because minims group in twos at this moment in the piece. In this case the cadence is considerably weakened both by its metric placement and by the lower voice’s abrupt leap away from the cadential pitch, A3, to D4. This example reiterates the fact that the perfection phase alone determines a suspension’s metric placement. Furthermore, this is equally true of binary and ternary suspensions. Examples 9 and 10 serve as exceptions that prove the rule: the perfection phases of Renaissance suspensions tend to align with metrically strong positions, whereas in these two examples, the contrapuntal cadences are weakened by the weak metric placement of the perfection phases.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Bus1001d
The second scenario where the dissonance phase of a ternary suspension does not occur on the second beat of a group of three is in chains of suspensions. It is easiest to understand the structure of chains when they are composed of binary suspensions; for this reason, I will show a binary chain first (Example 11), then a ternary one (Example 12). In a chain, the resolution phase of one suspension also serves as the preparation for the ensuing suspension, circumventing the first suspension’s perfection phase in the process. All the suspensions in a Renaissance chain, save the last one, are missing their perfection phases, which makes chains such rhetorically strong figures. This also demonstrates the theoretical value of the perfection phase, because it underscores the idea that all but the last suspension in Renaissance chains are incomplete and are therefore fully dependent on the last in the chain. Each suspension creates the potential for a cadence to the pitch suspended in the dissonance phase. As the chain continually forestalls perfection by introducing more dissonances, cadential expectations are simultaneously frustrated and recalibrated. No passage of Renaissance music illustrates this better than Orlando di Lasso’s fifth texted duet, in which a chain of six suspensions sets the word malum (“evil”), as shown in Example 11. Peter Schubert has highlighted the link Meier made between repetition and evil and suggests that this passage’s use of repetition is therefore a madrigalism (Schubert 1995, 18; Meier 1988, 243–245). Furthermore, this passage communicates the meaning of the text given the exceptionally high number of possible cadential goals that are eluded before a sixth one is finally realized. This is a good example of how expecting a cadential perfection at the end of every Renaissance suspension can be a useful and engaging default hearing, even when that expectation is (in this case, repeatedly) not fulfilled. I explore this idea in more detail in the next section.
Example 12 shows a chain of ternary suspensions from the Sanctus of Josquin’s Missa De beata virgine. It may seem peculiar to call a group of just two suspensions a “chain,” but this is entirely accurate. The essential characteristic of a chain is that its suspensions overlap, and crucially, that a perfection phase is necessarily omitted by the joining of two links in the chain. Only the first three phases are present in the suspension beginning in m. 83 of Example 12. Note that while the dissonant interval (D4 against C4 or likewise against E4) may appear to resolve on the last minim of m. 83 (when the D4 moves down by step to C4), this minim C4 is actually an ornamental consonant anticipation of the true resolution phase, which falls on the downbeat of m. 84. This suspension does not end in a cadence because it does not proceed to a perfection phase. Instead, the next suspension comes to fruition and attains the true harmonic goal of the chain. Backtracking from the perfection phase, this explains the otherwise uncommon metric placement of the first suspension in the chain, whose dissonance phase is on beat three of m. 83 (as opposed to the standard beat 2), as labeled in Example 12.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Jos0303d
Chains of suspensions interact with the meter differently depending on whether they are composed of binary or ternary suspensions. In cases involving binary suspensions, such as in Example 11, each link of the chain has the same relative metric profile; at the rate of the CR, a regular alternation of dissonances giving way to consonances is set on a grid of strong and weak metric positions. But with chains of ternary suspensions like that from Example 12, the alternation of dissonances and consonances occurs in a strong-weak-weak metric context, so the dissonance phase, like all other phases present, repeatedly shifts its metric position by one unit with each new link in the chain.
As mentioned above, an agent is usually twice the value of the basic durational unit of its suspension because it tends to span the dissonance and resolution phases. An entirely viable (albeit less common) situation involves the agent moving at the beginning of the resolution phase, as in the suspension with its resolution phase on the downbeat of m. 84 in Example 12 (the C–A motion in the bass voice). This contrapuntal possibility is often called a “change-of-bass suspension.”
5. Musical Expectation
It is useful to expect a contrapuntal cadence at the end of every Renaissance suspension, both when that expectation is realized and when it is not. This expectation is the logical extension of acknowledging the presence of the perfection phase. To borrow the words of Margaret Bent, “it is not so much a question of what we see but of how we look, not of what we hear but of how we listen,” (1998, 31). Of course, there are non-cadential suspensions that are not part of a chain of suspensions, but these cases are less common in the Renaissance repertoire found in the JRP (which does not contain any late-Renaissance works). Those that are found can often be understood as cases of cadential evasion. In Gioseffo Zarlino’s discussion of cadential evasion, he includes a thirty-six-measure example containing twenty-two suspensions. Of these, only the last one proceeds to its perfection phase, concluding the example. His prose explanation is telling: “Therefore let it suffice to say that a cadence is evaded, as I said, when the voices give the impression of leading to a perfect cadence, and turn instead in a different direction,” (Zarlino 1558, 151–153). While Zarlino’s definition of a cadence does not necessarily require a suspension, this is the primary means of creating a cadence. Moreover, it is clearly the main syntactical element with which his example of cadential evasion engages in order to create cadential expectation.
I use the term “cadence” quite loosely throughout this article, and it includes many contrapuntal gestures that would add only very subtle punctuation to a musical form. Turning again to Zarlino, his comparison of the Renaissance musical cadence to a period of grammatical punctuation is apt:
A cadence is a certain simultaneous progression of all the voices in a composition accompanying a repose in the harmony or the completion of a meaningful segment of the text upon which the composition is based. We might also say that it is a sort of termination of part of the harmonic flow at a midpoint or at the end, or a separation of the main portions of the text . . .19 The cadence has a value in music equivalent to the period in prose and could well be called the period of musical composition (1558, 142–144).
So when I say that all suspensions are cadential by default, it is analogous to calling a period conclusive. Whether that period concludes a stray sentence or an entire novel, however, plays an enormous role in the interpretation of its rhetorical weight.
To recognize the perfection phase as an essential component of complete Renaissance cadences is to attribute cadential weight to suspensions by default. This could have a substantial impact on the way editorial accidentals are applied, as shown briefly in Example 9. Another example of this impact is in the Gloria of Josquin’s Missa De beata virgine shown in Example 13. Here, the altus’s minim F at the end of m. 27 should arguably be raised to F$$\sharp$$ to properly approach the expected perfection on the downbeat of m. 28. The approach to this moment strongly suggests a cadence: the superius descends from D5 to a unison perfection between the upper two voices on G4 and then rests. However, the bassus evades its standard resolution down a fifth (or up a fourth), causing this potentially cadential moment to be evaded, which is presumably the reason this edition from the JRP omits editorial accidentals here. But failing to raise this F destroys the phrase’s potential for a cadence before the E in the bassus even starts. Put another way, using an F$$\natural$$ here eliminates the harmonic and syntactic intrigue of the bassus’s move to E. Recognition of the integral role of the perfection phase allows for a more accurate rendering of such cadential evasions.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Jos0303b
6. Alternative Explanations
It can be difficult at first to accept that the dissonance phase of a suspension can fall on a weak beat. An initial reaction of this sort is understandable, as this notion contradicts the definition of a suspension as given in almost all treatises and textbooks for over 500 years. One might refute the idea that a suspension can fall on a weak beat with either of two arguments. First, one might argue that the second beat in a ternary meter is of intermediate strength, and so is actually stronger than the third beat. The main problem with this claim stems from the incorrect assumption that Renaissance syntax is the same as tonal syntax with respect to suspensions. The case for the supposed metric strength of beat two is usually based on the fact that beat two often carries the dissonance phase of a Renaissance ternary suspension. While this is true, it does not follow that beat two is strong, because Renaissance ternary suspensions necessarily place their dissonance phases on beat two to accommodate the perfection phase in its preferred metrically strong position. Since the perfection phase commands the metric placement of a Renaissance suspension, a beat is not strong simply because it contains a dissonance phase. Furthermore, beat three can support the dissonance phase of a ternary suspension (such as in m. 83 of Example 12) despite being a definitively weak beat.
The second argument used to dismiss Renaissance ternary suspensions is the idea that any suspension dissonance on beat two must be a case of an unnotated change in the metric organization, or hemiola. Given two measures in $$3\atop1$$ with the dissonance phase of a suspension falling on beat two of the second measure, one could hear the meter as being in three binary groups of two semibreves each. This hearing can quickly run into problems, however, when we have more than one ternary suspension in close proximity. Example 14 from Josquin’s Gloria from the Missa Da pacem, is a case in point. The first downbeat, in m. 79, is the perfection of the preceding cadence and also the moment the effective meter shifts from $$4\atop2$$ to $$3\atop1$$. If we insist on hearing the dissonance phase of the first ternary suspension (the first red notehead) as metrically strong, this analysis begins reasonably enough and is at least possible through m. 83. Problems arise when the lower two voices repeat the same two-voice module as the upper two voices (i.e. mm. 83–86 echo mm. 80–83), but inexplicably with a reversed metric interpretation; what was strong is now weak, and vice versa. When the very same ternary suspension returns in m. 85 (the second red notehead), its dissonance phase falls on a weak beat if we stick to the same strong-weak grid (i.e. 1, 2, 1, 2, . . . , shown at the bottom of the excerpt). In short, no consistent binary hearing makes sense for this entire passage. The only steady metric hearing that preserves the metric strengths of analogous elements in the repetition in mm. 83–86 is the notated $$3\atop1$$. While larger and smaller metric groupings are possible, I only group semibreves in this excerpt because this is the unit of time that corresponds to the phases of the suspensions, and by extension also to the CR.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Jos0302b
One might argue that the music oscillates between ternary and binary metric organizations as necessary to keep the dissonance phases of every suspension on strong beats through metric reinterpretation. Example 15 annotates the same excerpt, marking the beats of a uniformly ternary hearing above the staff and that of a hearing that repeatedly shifts between ternary and binary groupings below the staff. The bold numbers in the lower beat annotations indicate changes in meter in this hearing. The straight ternary reading on the top is definitely the simpler of the two. What musical event in m. 81 could suggest that its third beat should be strong? Especially for musicians reading from parts, not scores, this is difficult to justify. While it is certainly possible to sing the passage this way, an analyst cannot base such a decision on the problematic premise that the dissonance phase should be strong. Hemiola can occur in Renaissance music, but it should be seen as considerably rarer than ternary suspensions.

7. Metric Ambiguity
Understanding passages in O mensuration (or any other sign or combination of signs that results in groupings of three imperfect semibreves) is critical for two reasons. First, this is where most Renaissance ternary suspensions are found, and second, these passages are easy to misinterpret because there are three distinct combinations of meter and contrapuntal rhythm that can govern them. These three combinations appear in Table 2b–d. Modern editions of Renaissance scores usually interpret O mensuration with the $$3\atop1$$ time signature. If the contrapuntal rhythm is equal to the semibreve (Table 2b) then suspensions found here will be ternary. If, instead, the contrapuntal rhythm is equal to the minim, suspensions could be binary (Table 2c) or ternary (Table 2d), depending on whether one hears minims grouping in twos or threes. In many cases, such suspensions are ambiguous because a reasonable case can be made for either interpretation. I distinguish between examples c and d in Table 2 by giving them $$3\atop1$$ and $$6\atop2$$ time signatures respectively, but one will notice that the passages are otherwise almost identical. One suspension-based means of deciding between $$3\atop1$$ and $$6\atop2$$ hearings is to listen for the less common suspensions whose perfections line up on minims of intermediate strength. If a perfection is heard on the third or fifth minim of such a measure, this points to a binary classification of the suspensions and a $$3\atop1$$ hearing; a perfection on the fourth minim suggests ternary suspensions and a $$6\atop2$$.
The differentiation between binary and ternary suspensions also highlights some points of metric ambiguity in Renaissance music. Josquin’s Alma redemptoris mater carries the O mensuration sign, the modern score is notated with a $$3\atop1$$ time signature, and crucially, the contrapuntal rhythm of the excerpt is equal to the minim (Josquin, n.d.). As most do, the suspension in mm. 35–36 of Example 16 aligns its perfection phase with a metrically accented semibreve on the downbeat of m. 36; its dissonance phase occurs two minims earlier on beat three in m. 35. But the two suspensions in m. 34 are of particular interest. The second suspension in m. 34, whose dissonance phase is marked red in Example 16, has a metric placement just like that of the following suspension whose perfection phase occurs on the downbeat of m. 36. These are both analyzed by the dissonance classifier as binary, because the basic units of the suspensions are minims, and minims group in twos in $$3\atop1$$. While the first suspension in m. 34 has the same durational profile as the others, its metric placement is very different. This first suspension, marked blue, places its perfection phase on a weak metric position. The perfection (the unison on G4 halfway through m. 34) is metrically weakened, as it lands on the weak part of the second beat. However, if we consider this suspension in $$6\atop2$$ instead of $$3\atop1$$, the perfection would land on the fourth of six minims, a relatively strong metric position. For this reason, the dominant interpretation of this suspension is as ternary.
With the potential for hearing this music in $$6\atop2$$ in mind, we can re-examine the two other suspensions in Example 16, both of which are labeled with a lowercase “s” and “g” denoting their identification as binary suspensions. In this considerably more common scenario (where the basic durational unit of the first three phases of the suspension is the minim, and the perfection phase lines up on the downbeat) the suspension by itself is actually metrically ambiguous. This is because a suspension of this kind could equally well articulate $$3\atop1$$ and $$6\atop2$$ meters. While I agree that $$3\atop1$$ is the most appropriate modern time signature for this excerpt, it is important to note the metric malleability of this passage and others like it. In cases like this one, where a suspension could be heard as binary or ternary, the dissonance classifier defaults to the more common binary label. The dissonance classifier conveys the metric ambiguity in its analysis of the excerpt in Example 16 as a whole, with the juxtaposition of ternary and binary suspensions in such close proximity and with identical durational profiles. Given the immense influence that dissonance treatment and rhythm have on the aural discernment of meter, this underscores the need to distinguish between binary and ternary suspensions when analyzing Renaissance meter.
As an interesting side-note concerning Example 16, the two suspensions found in m. 34 do not coalesce into a chain. This is because they are spaced too far apart for the resolution of the first suspension to serve a dual function as the preparation of the second suspension. To a certain extent, they still overlap because the perfection phase of the first suspension doubles as the preparation for the second. However, the rhetorical effect is decidedly not like that of a chain because the first suspension is able to realize its perfection phase.

http://verovio.humdrum.org/?k=ey&filter=dissonant%20–color&file=jrp:Jos2302
8. Suspension Classification in Broader Contexts: A Survey of Resources
Arthur Komar justifiably identifies suspensions as an invaluable component of musical analysis in his 1971 book, Theory of Suspensions, but his exclusive focus on tonal music and preference for dissonance in duple meter (a proclivity nearly ubiquitous among writers on dissonance treatment) result in the omission of Renaissance ternary suspensions. With the goal of assessing the general knowledge of the field on suspensions, I consulted over eighty sources including historical counterpoint and harmony treatises, modern textbooks, and musical encyclopedias. The results were similar across primary and secondary sources; there is little accurate information about Renaissance-style ternary suspensions. Only five sources acknowledge them at all, and even these stand-out sources overlook many important details about how Renaissance ternary suspensions function.
Despite omitting explicit description of ternary suspensions, a couple of the more thorough counterpoint textbooks that are particularly rich in repertoire citations do include examples of them. Serge Taneiev’s Convertible Counterpoint in the Strict Style falls in this category (1909, 139). Most authors of textbooks and treatises pertaining to Renaissance counterpoint entirely forgo discussion of ternary suspensions, generally as part of a larger omission of a discussion of triple meter. The tonal counterpoint manuals that do include metric guidelines about ternary suspensions invariably insist that the dissonance phase should be metrically strong. For example, in his 1904 book, Tonal Counterpoint, Walter Spalding provides many more examples of ternary suspensions than most authors and all of these put the dissonance on beat one of a $$3\atop4$$ measure. His primary discussion of them is reproduced in Example 17 (1904, 117).
“at (a) we have a suspension with normal resolution:
at (b) an interpolated note which is a factor (the fifth) of the harmony delayed by the suspension; and at (c) a changing note, used in the normal way—that is, it is taken by a leap of a third and resolves diatonically to a note within. To secure an effective cadence in this order, it is always necessary to adopt an ornamental resolution for the suspension [see Example 17].”
However, the juxtaposition of stylistic influences obscures Spalding’s treatment of ternary suspensions. None of these examples constitutes a cadence in the tonal sense; instead the examples in the second set demonstrate melodic variations of a Renaissance cadence. The metric placement of his ternary suspensions, however, conforms to the tonal standard, meaning that he is mixing a Renaissance definition of cadence with a tonal concept of metric placement. My reservations about the exposition of ternary suspensions notwithstanding, Spalding’s counterpoint textbook does explicitly acknowledge ternary suspensions, unlike most authors. It likewise provides multiple examples including more extended passages of two-voice counterpoint in ternary contexts featuring multiple tonal ternary suspensions, such as that reproduced in Example 18 (1904, 118). Furthermore, given the title of his book, Tonal Counterpoint, the fact that he omits discussion of Renaissance norms is understandable as they are mostly outside his scope.
The pure species approach to suspensions is relatively unnatural for Renaissance syntax, because in this idiom suspensions primarily serve to drive toward an immediately ensuing contrapuntal cadence. As such, Renaissance suspensions, binary and ternary alike, gravitate towards the ends of phrases rather than being used right at the outset of a passage as in Example 18. Even chains of suspensions are not common at the beginning of a passage in Renaissance music. Going further, the basic rhythmic profile of Example 18 is uncharacteristic of Renaissance ternary suspensions because both voices tend to move by contrary motion in the perfection phase. This means that, even in ternary cases, the agent is still typically twice the value of the basic durational unit of the dissonant portion of its patient, because it usually spans the dissonance and resolution phases in unornamented cadences.
The five authors of counterpoint textbooks that do address Renaissance ternary suspensions are: Olivier Trachier (1999, 31), Robert Stewart (1994, 71–72), Charlotte Smith (1987), R. O. Morris (1922, 39), and Johannes Tinctoris (1477, 115–126).20 As Tinctoris is the most thorough, his discussion of suspensions is worth examining in more detail. He spends a large portion of Book II of the Liber de arte contrapuncti describing a great variety of mensural situations (including mixed mensurations) in which binary and ternary suspensions occur. This may have been intended as a demonstration of his learning, given that mastery of the mensural system was considered the pinnacle of musical erudition in his time. Tinctoris does not explicitly distinguish between binary and ternary suspensions, but since he is specific about the mensuration signs and note values used in different scenarios, and since he provides musical excerpts as examples, it can be discerned when he is discussing each type of suspension.
It is noteworthy that Tinctoris generally describes the metric placement and duration of the agent, not of the patient (though we generally think of the latter as the suspension itself). The agent is usually the tenor in his examples, in keeping with Tinctoris’s consistent tenor orientation in the measuring of interval successions, and in determining of mode in a polyphonic piece. The dissonance classifier described above follows Tinctoris’s teaching on this point and labels suspensions as binary or ternary primarily according to the agent’s contrapuntal profile.
Chapters 23–28 of Book II comprise the core of Tinctoris’s advice on how to use different dissonance types idiomatically. Below, I clarify the details of Chapter 23, which provides the best description of how Tinctoris conceives of suspensions. (Chapters 24–28 focus on dealing with complexity added by mixed-mensuration settings.) Book II is rather dense, making even a translation very difficult to unpack. Furthermore, the fact that the twenty-nine-measure example that accompanies Chapter 23 is unlabeled makes it more difficult to ascertain exactly how the three-voice piece exemplifies what he describes in prose.
The first sentence serves to permit weak dissonances such as passing and neighbor tones that are no more than half of the duration of the note that they are dissonant against, and also fall on a metrically weak portion of that longer note.21 For example, a weak minim in one voice can ornament a semibreve in another.
Next, Tinctoris turns to suspensions, so all of the “discords” in the following excerpt refer to suspensions, and more specifically, the patients of suspensions. The note values he describes are mostly for the agents of suspensions. Every time he refers to major and minor prolation here, it describes metric scenarios where there are three or two minims to the semibreve respectively. When Tinctoris writes of “two minims, existing as a unit or separately in the same place,” this means that the musical realization can either be with a single semibreve, or with two consecutive minims repeating the same pitch. When he explains that a syncopation (suspension) can be “of a minim by itself, and, additionally, in minor prolation above the first part of the two semibreves,” this makes it explicit that suspensions can happen at three distinct timescales. Finally, when Tinctoris writes of “a descent into some perfection” made by many minims or semibreves, he is addressing the case of chains of suspensions.
On the other hand, indeed, not only in major prolation, but also in minor,22 a discord is almost always taken above the first part of the first of two minimae, existing as a unit or separately in the same place, or of a minima by itself, and, additionally, in minor prolation above the first part of the two semibreves, also existing as a unit or separately in the same place, immediately preceding some perfection. Further, if, not only in major prolation but also in minor, a descent into some perfection is made by many minimae or, additionally, in minor prolation by many semibreves, a discord by syncopation on the first part of any one of these is also most frequently allowed, as [Example 19.]

Notice that Tinctoris does not specify the metric placement of the suspensions. Just like Vicentino and Burmeister, he allows for suspensions at three timescales: those with CR units equal to the semiminim, the minim, or the semibreve. This is the first written precursor to Vicentino and Burmeister’s examples we saw in Examples 6 and 7. Furthermore, he always describes suspensions as coming just before a perfection. While he does not explicitly mention binary and ternary suspensions, the fact that his prose omits any discussion of metric placement makes his definition of a suspension equally appropriate for binary and ternary varieties. I have added editorial ficta to Tinctoris’s example to make the perfections more obvious.
Two ternary suspensions occur in Example 19, in mm. 17–18 and 19–20. Both arise in the context of semibreve CR units. Chains of binary suspensions appear in mm. 6–7 and 21–22 with semiminim CR units, and in mm. 25–26 with minim CR units. There are double suspensions and single suspensions with multiple agents. Notably, all sixteen suspensions in this example are either cadential (just like Vicentino and Burmeister’s suspensions in Examples 6 and 7 above) or parts of chains of suspensions that end in cadences. Overall, this passage does an excellent job of exemplifying both the variety often found in Renaissance suspensions and their consistently cadential function.
While Stewart, Smith, Trachier, Morris, and Tinctoris rightly acknowledge Renaissance ternary suspensions and, for the latter three, demonstrate their standard metric placement, they do not address why the dissonance phase tends to occur on beat two. This point can be elusive when one fails to distinguish between binary and ternary suspensions, to consider the current CR unit, or to recognize that chains of suspensions constitute a special case. In her discussion of dissonance placement in triple meter, Margarita Merriman addresses her student readers by saying: “The student can be forgiven for some bewilderment at this point concerning what constitutes normal usage [of dissonances] in triple meter. He is advised to analyze works in both fast and slow triple meter and draw his own conclusions” (1982, 93). Similarly, Stewart’s (1994, 71–72) counterpoint textbook suggests that there is little rhyme or reason behind their metric placement, simply stating that, in certain instances of triple meter, “[the dissonance phases of] suspensions occur on all beats.” But the three unidentified examples he cites are all actually instances of chains of suspensions, which are the primary cause of variation in the metric displacement of ternary suspensions, as seen earlier. It is hoped that this article provides a clearer explanation of what ternary suspensions are and how they work.
9. Ternary Suspensions in Tonal Music
The reader may have noticed that almost all of my examples have been from earlier Renaissance composers. The general decrease in mensural variety that took place over the course of the Renaissance does mean that there are fewer ternary suspensions in late-Renaissance works, simply because there are fewer passages where the CR unit groups in threes (that is, passages with a ternary tactus). But naturally these ternary suspensions still occur, such as in the excerpt from Giovanni da Palestrina in Example 20.
It remains an open question how and when standard suspension syntax shifted from the end-accented Renaissance type that drives to the perfection phase to the middle-accented tonal variety that generally omits a perfection phase. In this section, I will offer some preliminary thoughts on when and how this took place. While the transition has implications for both binary and ternary suspensions, it has a lesser impact on binary suspensions. In both Renaissance and tonal music, the dissonance phase and the perfection phase (to the extent that there is one in tonal music) are typically two CR units apart, which gives both suspension styles similar metric placement and strength in binary contexts. Therefore, examining ternary suspensions is the most revealing way to determine when the default syntax of suspensions began to change.

In tonal music, a suspension can integrate into the harmonic fabric of a cadence, but its presence is not essential as it is in Renaissance music. Even in the case of cadential $$6\atop4$$ chords, the dissonant fourth is not necessarily approached in the manner of a suspension, and when it is, the voice with the dissonant fourth is usually subordinate to the main melodic line descending from $$\hat3$$ to $$\hat2$$ to $$\hat1$$. The general absence of a perfection phase leaves tonal suspensions in need of a different phase of reference for their metric orientation and the dissonance phase fulfills this role. Monteverdi’s madrigals appear to be transitional with respect to this aspect of musical syntax. Particularly in Book Eight, there is an abundance of ternary suspensions roughly evenly distributed between the standard Renaissance fashion and an unornamented precursor to the tonal variety. The latter consists of a compromise between the Renaissance need for the perfection phase to be metrically strong and the tonal pull for the dissonance phase to be so. Monteverdi often makes both phases metrically strong in a ternary meter by elongating the dissonance phase, as in Example 21, but without Spalding’s ornamentation shown in Example 17.

This can also occur in the context of music that sets up the regular expectation for uneven rhythms such as the passage in mm. 122–128 in Example 22, which repeatedly makes use of the following rhythmic pattern: breve, semibreve, dotted semibreve, minim, semibreve (breve, whole note, dotted whole note, half note, whole note). While I present Monteverdi’s suspensions as occupying an intermediary stance between Renaissance and tonal standards, they represent but one small portion of this important transition. A more thorough analysis of precisely how and when composers transitioned from Renaissance to tonal ternary suspensions is left for another study. It is interesting to note that the dissonance classifier labels the suspension in Example 21 as binary but the one in Example 22 as ternary. Due to the elongated duration of the dissonance phase, the CR is not entirely clear, so the analysis tool reverts to the default binary label for the former. In the latter, the different rhythm in the agents helps the tool interpret this as a ternary suspension. While it seems that both of these should intuitively be ternary suspensions, the methodology for such an analysis is not clear given that a regular value for the CR is somewhat difficult to pin down in these examples.

10. Ternary Suspensions as Stile Antico References
While the dissonance phase of a tonal ternary suspension is usually metrically accented, one occasionally finds instances where the dissonance is on the second unit of a group of three. Bach’s F$$\sharp$$-minor fugue from Book I of the Well-Tempered Clavier is a good example.23 The subject ends in a prominent $$\hat2$$–$$\hat1$$ motion, marked red in mm. 3–4 of Example 23, in the manner of a tenorizans cadential-voice function. When it reappears as a real answer, it is naturally complemented with a suspension patient in the countersubject. The string of blue notes in Example 23 contains all four phases of this ternary suspension. Due to the presence of a Renaissance-style ternary suspension in this all-important contrapuntal pair, this fugue is replete with old-fashioned ternary suspensions of this kind.
Bach’s suspension treatment in this fugue amounts to a Renaissance reference in a work that still clearly asserts its tonal nature. The Grove Music online encyclopedia defines the stile antico as “the presence of ‘old-fashioned’ features associated with Renaissance polyphony, such as alla breve metre . . . , imitative textures, a traditional approach to dissonance, scoring for full choir . . . and a balanced melodic style reminiscent of Palestrina’s” (Miller 2017). While the use of Renaissance-style ternary suspensions may fall under the broad aegis of “a traditional approach to dissonance” in the quote above, this very specific stylistic borrowing is a hitherto overlooked component of these sorts of references.
11. Suspensions and Tonal Syntax
My focus here has been on Renaissance-style ternary suspensions, but it is also worthwhile to re-examine suspensions in tonal music. The concept of contrapuntal rhythm that is essential to my approach to understanding Renaissance dissonance is not easy to apply to tonal music. Harmonic rhythm cannot fill the same role as CR because, in practice, they are phenomena with little in common. Furthermore, discerning the harmonic rhythm presents difficulties and ambiguities of its own.
II7 chords are an interesting case. Chordal sevenths (of chords that are not dominants) are typically prepared in tonal music, which suggests that the II7 chord would be metrically accented because that is the standard case for the dissonance phase of a tonal suspension. Nevertheless, some variety exists because II7 chords (typically in first or second inversion) can be found in weak metric positions. Example 24 includes excerpts taken from Bach chorales and shows II7 chords in weak metric positions with a prepared chordal seventh.24 In a $$4\atop4$$ context and a harmonic rhythm equal to the quarter note, II chords and their chordal sevenths—integrated by means of suspensions—will typically fall on a weak beat to allow the dominant arrivals that immediately follow them to be metrically accented. If the dominant takes up two beats, an ensuing tonic chord can also be metrically strong. A conventional technique involves a cadential $$6\atop4$$ chord (or occasionally a $$5\atop4$$ sonority) followed by a dominant seventh, each lasting a beat. This is similar to Renaissance suspension syntax because a goal is identified, and then the harmonic material leading up to that goal fills up the immediately preceding space in the music, falling in whatever metric context the established meter demands. For Renaissance music, I have shown that the goal is the perfection phase of the suspension. For tonal music, this goal is usually either the dominant or the tonic arrival in a cadence. It is noteworthy that harmonic syntax had changed so much by the time Bach was composing that none of the tonal cadences in Example 24 would constitute Renaissance cadences in the strict sense. This is because the voice that would fulfill the cantizans cadential-voice function (in these cases, the tenor) does not realize the perfection that one would expect in Renaissance music (by resolving the leading tone up by step), but rather skips down to $$\hat5$$ or goes to $$\hat3$$ in the interest of having a complete tonic triad at the end of the cadence.
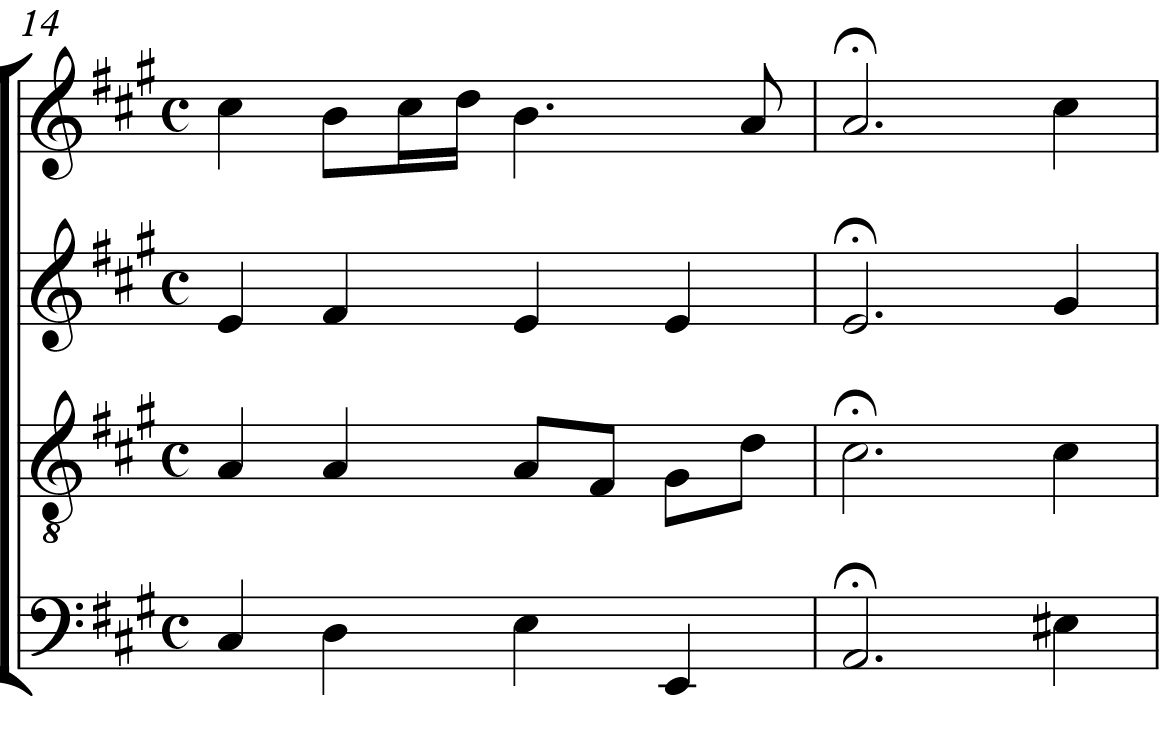
http://verovio.humdrum.org/?file=g:craigsapp/bach-370-chorales/kern/chor091.krn&filter=satb2gs

http://verovio.humdrum.org/?file=g:craigsapp/bach-370-chorales/kern/chor121.krn&filter=satb2gs

http://verovio.humdrum.org/?file=g:craigsapp/bach-370-chorales/kern/chor312.krn&filter=satb2gs

http://verovio.humdrum.org/?file=g:craigsapp/bach-370-chorales/kern/chor347.krn&filter=satb2gs
Example 24. Four passages from Bach chorales, each featuring a suspension with the dissonance phase on a weak beat, coinciding with a II chord just before a dominant arrival.
In Examples 11 and 12, we saw how a chain of suspensions occurs when a resolution phase of a suspension serves a dual function as the preparation of the next suspension. Put in terms of the norms of Renaissance music, we expect a perfection phase to conclude the first suspension, but the dissonance phase of a second suspension arrives instead. In the tonal suspensions in Example 24, however, after the first suspension’s dissonance phase, one may reasonably expect a resolution phase; instead, we hear a second dissonance phase, so the overlap between the two suspensions is something of a contracted chain. That is, instead of hearing the dissonance-resolution-dissonance phase pattern, we hear two dissonances with no intervening resolution. Why would we hear this as a chain of suspensions rather than as a single suspension with an extended dissonance phase? From a tonal perspective, this is partly because the harmony changes. Returning to the concepts of agents and patients, in a II7 chord where the seventh is prepared, $$\hat1$$ is the patient and $$\hat2$$ is the agent. In an intervallic sense, $$\hat3$$ is not dissonant in a cadential $$6\atop4$$ chord. Again the patient is $$\hat1$$ but the agent is $$\hat5$$. Assuming that the II chord is in first or second inversion (as is typically the case), the agents of these two suspensions will necessarily come from different voices. I would argue that this adds to the impression that there are indeed two distinct suspensions, not just one with an extended dissonance phase, though the distinction is perhaps a small one. Assuming one does hear two different suspensions, it is noteworthy that there is no sense of metric reinterpretation as would be produced by two successive strong beats. This is because, in tonal and Renaissance music alike, the dissonance phase of a suspension is not necessarily metrically stressed. That is why none of the excerpts in Example 24 produce a jarring metric effect but instead come across as artless tonal syntax.
As a final point about Example 24, there appears to be a strong correlation between these weak-dissonance-phase suspensions and the melodic ornamentation of the metrically accented dominant arrival. I have only shown four examples, but there are several more in Bach’s chorales. Future studies will hopefully go beyond simply counting dissonance types to uncover more revealing correlations between dissonance treatment, meter, harmony, melody, and countless other musical domains for a given musical style or repertoire.
Conclusion
In summary, by highlighting the case of ternary suspensions, I have shown the fundamental flaws of the idea that the dissonant portion of a suspension is necessarily metrically strong. Despite being slightly more common than the historically well-documented “fake” suspension, ternary suspensions have been generally overlooked in centuries of counterpoint treatises and textbooks. The locus of metric orientation in binary and ternary Renaissance suspensions alike is the metrically strong fourth phase, the perfection.
I have also identified some particularities about Renaissance suspensions. Occasionally, a weak temporal placement of the perfection phase is a means of reducing the rhetorical weight of an interior cadence. In chains of Renaissance ternary suspensions, the units of the suspensions are out of phase with the prevailing meter, thereby adding drive to the cadential perfection that concludes the chain and resolves the harmonic and metric conflict. In addition, the placement of suspensions can accentuate the metric ambiguity between $$3\atop1$$ and $$6\atop2$$ hearings of Renaissance music, so refined knowledge of suspensions can help make us more attentive to such musical subtleties.
Ternary suspensions were first recognized in 1477 with Tinctoris’s Liber de arte contrapuncti and then almost entirely forgotten in theoretical writings. Given the frequency of their use, as well as the important and very audible stylistic particularities they bring with them, the knowledge and discussion of ternary suspensions have a place in the mainstream teaching and analysis of Renaissance counterpoint. Generally speaking, the corpus-study portion of this article demonstrates how music information retrieval can weigh in on pedagogical concerns, such as the question of what to focus on in textbooks.
The way ternary suspensions function is an important contrapuntal means of distinguishing between Renaissance and tonal syntax. As tonal syntax moves away from intervallically defined cadences, suspensions get largely dissociated from their previously standard perfection phases. In the absence of the metric orientation that the perfection phase provides Renaissance suspensions, tonal ones gravitate to the dissonance phase, often favoring it to be metrically strong. But as we saw, there are exceptions to this. Monteverdi’s eighth book of madrigals seems to represent a critical point in the transition from Renaissance to tonal ternary suspensions, though the exact origins and epicenter of this seismic shift in musical syntax are yet to be determined. Finally, the use of a Renaissance ternary suspension in an otherwise tonal piece can function as a stile antico reference, and this observation may have an important impact on how we recognize and process references to Renaissance music.
The ability to distinguish between binary and ternary Renaissance suspensions and awareness of the perfection phase are manifestly critical to a thorough understanding of Renaissance syntax. While relatively easy to comprehend, the present focus on the perfection phase in the model of Renaissance suspensions does contradict some deeply and long-held assumptions common in the field about suspension syntax and accentuation. It is my hope that our fluency with Renaissance music will improve as we rediscover this knowledge.
Alexander Morgan examines dissonance treatment, cadences, and contrapuntal rhythm as components of style change in the music of the Renaissance and Early Modern periods. He is interested in in corpus studies and has created several automated analysis tools to support his findings empirically, including for the Humdrum and VIS analysis platforms. Alongside his repertoire research, Alexander is also a specialist in interval-succession treatises of the Renaissance, especially those of Tinctoris and Pontio. His primary findings on Tinctoris will be published as a chapter in a forthcoming book on the theorist. The common thread that runs throughout his work is a focus on counterpoint as a primary structural and expressive domain. Alexander currently works as a software developer in New York City.
References
Antila, Christopher, Alexander Morgan, et al. 2016. VIS Framework (version 3.0.3). Python. Montreal: McGill University.
Arlettaz, Vincent. 2000. Musica Ficta: Une histoire des sensibles du XIIIe au XVIe siècle. Pierre Mardaga: Sprimont, Belgium. Originally published as a dissertation: 1998. “Etudes sur l’apparition du langage tonal.” L’université de Paris-IV Sorbonne.
Artusi, Giovanni Maria. 1598. L’arte del contraponto. Venice, G. Vincenti. Accessed on www.gallica.bnf.fr on September 22, 2017.
Bent, Margaret. 1998. “Grammar of Early Music: Preconditions for Analysis.” In Tonal Structures in Early Music, edited by Cristle Collins Judd, 15–59. London: Garland Publishing.
———. 2003. “Ciconia, Prosdocimus, and the Workings of Musical Grammar as Exemplified in O felix templum and O Padua.” In Johannes Ciconia, musicien de la transition, edited by Philippe Vendrix, 65–106. Turnhout: Brepols.
Burmeister, Joachim. (1606) 1993. Musical Poetics. Translation by Benito Rivera. New Haven: Yale University Press.
Ceulemans, Anne-Emmanuelle. 1998. “Une étude comparative du traitement de la mélodie et de la dissonance chez Johannes Ockeghem et chez Josquin des Prez.” In Actes du XIe colloque international d’études humanistes. Edited by Philippe Vendrix, 707–753.
Cherubini, Luigi. 1851. Cours de contrepoint et de fugue. Second edition. Paris: Heugel et Cie Editeurs.
Cohen, David. 1993. “Metaphysics, Ideology, Discipline: Consonance, Dissonance, and the Foundations of Western Polyphony.” Theoria (7): 1–86.
———. 2001. “‘The Imperfect Seeks Its Perfection’: Harmonic Progression, Directed Motion, and Aristotelian Physics.” Music Theory Spectrum 23 (2): 139–169.
Dahlhaus, Carl. 1990. Studies on the Origin of Harmonic Tonality. Translated
by Robert O. Gjerdingen. Princeton: Princeton University Press.
DeFord, Ruth. 2015. Tactus, Mensuration, and Rhythm in Renaissance Music. Cambridge: Cambridge University Press.
Fuller, Sarah. 1993. “Tendencies and Resolutions: The Directed Progression in ‘Ars Nova’ Music.” Journal of Music Theory 36 (2): 229–258.
Jeppesen, Knud. 1939. Counterpoint: The Polyphonic Vocal Style of the Sixteenth Century. Translated by Glen Hayden from the original Danish edition (Wilhelm Hansen, Copenhagen, 1931). Englewood Cliffs, New Jersey: Prentice Hall Inc.
Komar, Arthur. 1971. Theory of Suspensions: A Study of Metrical and Pitch Relations in Tonal Music. Princeton: Princeton University Press.
Lasso, Orlando di. 1973. Magnum opus musicum. Typeset by Carl Proske and edited by Franz Xaver Haberl. New York: Broude Brothers Limited.
Meier, Bernhard. 1988. The Modes of Classical Vocal Polyphony. New York: Broude Bros.
Merriman, Margarita. 1982. A New Look at 16th-Century Counterpoint. Lanham, MD: University Press of America.
Miller, Stephen. “Stile antico.” Grove Music Online. Oxford Music Online. Oxford University Press. Accessed on September 27, 2017.
http://www.oxfordmusiconline.com/subscriber/article/grove/music/26771.
Morgan, Alexander. 2017. “Renaissance Interval-Succession Theory: Treatises and Analysis.” PhD diss., McGill University.
———. “Humlib Dissonance Classifier: A New Tool for Renaissance Dissonance Classification.” In Proceedings of the 9th European Music Analysis Conference. Strasbourg: GREAM, forthcoming.
Morley, Thomas. 1952 (1597). A Plain and Easy Introduction to Practical Music. Edited by R. Alec Harman. London: J. M. Dent & Sons Ltd. (London: Peter Short).
———. 2000 (1595). First Book of Canzonets to Two Voyces. Edited by Bernard Thomas. London: London Pro Musica.
Morris, R. O. 1922. Contrapuntal Technique. Oxford: Oxford University Press.
Pugin, Laurent, et al. 2019. Verovio. [Music-notation software]: https://www.verovio.org/.
Sapp, Craig. 2019. Verovio Humdrum Viewer. [Online music typesetting and analysis software]:
http://verovio.humdrum.org/.
Schubert, Peter. 1995. “A Lesson from Lassus: Form in the Duos of 1577.” Music Theory Spectrum 17 (1): 1–26.
———. 2008. Modal Counterpoint, Renaissance Style, 2nd ed. New York: Oxford University Press.
Sigler, Andie, and Jon Wild. 2015. “Schematizing the Treatment of Dissonance in 16th-century Counterpoint.” In Proceedings of the International Society for Music Information Retrieval: 645–650.
Smith, Charlotte. 1987. A Manual of Sixteenth-Century Contrapuntal Style. Newark: University of Delaware Press.
Soderlund, Gustave. 1947. Direct approach to counterpoint in the 16th-century style. New York: F.S. Crofts.
Spalding, Walter Raymond. 1904. Tonal counterpoint: studies in part-writing. Boston: A.P. Schmidt. Accessed on September 12, 2017.
https://babel.hathitrust.org/cgi/pt?id=uc2.ark:/13960/t5h991c34;view=1up;seq=132.
Stewart, Robert. 1994. An Introduction to Sixteenth-Century Counterpoint and Palestrina’s Musical Style. New York: Ardsley House Publishers, Inc.
Taneiev, Serge Ivanovitch. (1909) 1962. Convertible Counterpoint in the Strict Style. Translated by G. Ackley Brower. Boston: Bruce Humphries (Moscow).
Tinctoris, Johannes. 1477. Liber de arte contrapuncti. Translated by Jeffrey Dean. Accessed on August 16, 2017.
http://earlymusictheory.org/Tinctoris/texts/deartecontrapuncti/.
———. (c. 1477) 1961. Liber de arte contrapuncti. Translated by Albert Seay. Rome: American Institute of Musicology.
———. (c. 1477) 1975. Liber de arte contrapuncti. In Johannes Tinctoris Opera Theoretica. Compiled by Albert Seay. n.p.: American Institute of Musicology.
Trachier, Olivier. 1999. Contrepoint du XVIe siècle. Paris: Durand.
Vicentino, Nicola. 1996 (1555). Ancient music adapted to modern practice (L’antica musica ridotta alla moderna prattica). Translated by Maria Rika Maniates and edited by Claude Palisca. New Haven, Yale University Press.
Zarlino, Gioseffo. 1968 (1558). Art of Counterpoint. Translated by Guy Marco and Claude Palisca, edited by Claude Palisca. New Haven and London: Yale University Press.
Notes
- This work was presented at the EuroMAC IX conference in 2017 and will be published in the forthcoming conference proceedings.
- I would like to thank Malcolm Sailor for bringing Renaissance ternary suspensions to my attention.
- http://josquin.stanford.edu/, accessed January 24, 2018.
- For other empirically minded studies of Renaissance dissonance, see Arlettaz 2000, Ceulemans 1998, and Sigler and Wild 2015.
- The complete dissonance analysis of any piece on the JRP website can be viewed by clicking on the “Dissonant: all dissonances labeled” button on the left-hand side of a desired piece’s page. An annotated score opens in a new tab using the Verovio Humdrum Viewer being developed by Craig Sapp, and Verovio, which is a project led by Laurent Pugin. http://www.verovio.humdrum.org, accessed September 23, 2017; www.verovio.org, accessed September 23, 2017.
- For a more modern explanation of agents and patients, see Schubert 2008, 76–77.
- The documentation for this analysis tool is available here: http://doc.verovio.humdrum.org/filter/dissonant/.
- DeFord acknowledges that it is possible for a polyphonic passage to project multiple and conflicting values for the contrapuntal rhythm. In situations such as this, the present study takes the strand of contrapuntal rhythm moving in the shortest durations to be the primary value. DeFord’s treatment of this effect of multiple simultaneous strands of contrapuntal organization is discussed in terms of tactus (the level at which the units of the contrapuntal rhythm group) and can be found in DeFord 2015, 82.
- In an effort to build on her work, chapter four of my dissertation (Morgan 2017) proposes a systematic method of determining the contrapuntal rhythm of a piece of Renaissance music, along with a code-based automation of this analytical process. The present paper addresses some of the issues that I encountered, particularly in situations where the units of contrapuntal rhythm group in threes.
- Throughout this article I use the mensural names for notes. In all the examples, these are converted to modern notation as follows: fusa = eighth note, semiminim = quarter note, minim = half note, semibreve = whole note, breve = breve.
- This does not include the “agentless suspension” category. For more on these dissonance types, see: Morgan, “Dissonance Classification,” forthcoming.
- Such as Cherubini 1851, 42–43 and 55 and Schubert 2008, 78. These are sometimes called “consonant fourth suspensions” such as in Stewart 1994, 61–62.
- For a dissonance corpus study done on the music of Palestrina and Victoria, see Sigler and Wild 2015.
- For more on the relationship between tactus and contrapuntal rhythm, see DeFord 2015.
- When $$3\atop1$$ is heard in conjunction with a contrapuntal rhythm at the minim, we are effectively hearing three binary groupings per measure, so it is a compound meter.
- For a general discussion of syntax in Early music, see Fuller 1993, 229 and Bent 2003. Concerning contrapuntal syntax at cadences, see DeFord 2015, 101–105.
- For more on cadential-voice functions, see Meier 1988, 90–101.
- Concerning the weakening of a cadence by its metric position, see DeFord 2015, 102–103.
- As a side note, throughout this article I assume that vocal music and instrumental music share the same core syntax with respect to suspensions. Nevertheless, some very minor differences may exist, such as the ways in which suspensions are ornamented.
- Margarita Merriman (1982, 92–93 and 146–149) also gives an example of a ternary suspension in her discussion of triple meter, but then she interprets binary suspensions in $$3\atop1$$ as ternary in her analysis of the metric placement of dissonances in the Hosanna of Palestrina’s Missa Regem Coeli. Merriman cites her teacher Gustave Soderlund for this take on suspensions in triple meter, and he likewise only addresses binary suspensions in $$3\atop1$$ meter where the contrapuntal rhythm is the minim (like in Example 2), so he does not address ternary suspensions in his handling of triple meter (Soderlund 1947, 65–66). Similarly, although Zarlino addresses ternary and binary mensurations in his handling of suspensions (syncopations), all of his examples are binary suspensions (1558, 120–123).
- Albert Seay’s translation of this first sentence reads: “In this simple counterpoint, on the one hand, discords are simply and absolutely prohibited, but in diminished they are allowed from time to time in a moderate amount; hence, it must be known, as I pass over the compositions of older musicians in which there were more discords than concords, that almost all more recent [musicians], not only composers but also those singing super librum, be it not only in major prolation, but also in minor, having put a concord on the first or another par of the minima and, in minor, additionally on the first or also on another part of the semibreve, they place a discord of this [value] or of a smaller note above that immediately following” (Tinctoris 1477, 113).
- That is, not only when there are three minims to the semibreve, but also when there are two.
- I would like to thank Jon Wild for bringing this example to my attention.
- All of these Bach choral excerpts are taken from the Kern Scores website. The whole chorales can be found at the links in the example captions.