Andrew Pau
Abstract
The Genevan music theorist Jean-Adam Serre (1704–1788) occupies a marginal position in the history of music theory. This article argues for a reevaluation of Serre’s harmonic theories, focusing on the second and third of the three Essais sur les principes de l’harmonie (Paris, 1753). The article compares Serre’s theories with those of his contemporaries such as Rameau and Kirnberger. Serre’s identification of the tonic, subdominant, and dominant triads as the only possible fundamental harmonies arguably presents an early form of functional theory, while his use of dual fundamentals for four-note chords prefigures modern theories of mixed function. In addition, Serre’s theories on the derivation of the minor mode reveal him to be a harmonic dualist writing more than a century before Hauptmann, Oettingen, and Riemann. For these reasons, Serre deserves to be more than a footnote in the history of music theory.
View PDF
Keywords and phrases: Serre, Rameau, Kirnberger, eighteenth-century harmonic theory, essentially fundamental bass, harmonic dualism.
The Genevan music theorist Jean-Adam Serre (1704–1788) was, like many other intellectuals of the Age of Enlightenment, a dabbler in numerous fields of study. In the encyclopedic Histoire littéraire de Genève published in 1806, Jean Senebier describes Serre as a “painter chemist and musician” whose scientific accomplishments included extracting brown enamel from platinum and drawing up a design for a barometer that was presented to the French Royal Academy of Sciences.1 Serre studied natural sciences at the University of Geneva and worked as a miniaturist in Vienna before moving to Paris in 1751.2 Two years later, in 1753, he published three essays on the principles of harmony (Essais sur les principes de l’harmonie), which engaged with the then-circulating theories of Jean-Philippe Rameau, Charles-Henri de Blainville, and Leonhard Euler, in addition to expounding Serre’s own harmonic theories. In 1763, after returning to Geneva, Serre published a second volume on harmony (Observations sur les principes de l’harmonie), which responded to the theories of Jean le Rond d’Alembert, Giuseppe Tartini, and Francesco Geminiani, among others. In the Preface to the Essais, Serre aligns himself firmly on the theoretical or speculative side of the historical musica theorica/musica practica divide, noting that “artists who are the most skilled in their art are [often] the least likely, or the least disposed, to give a genuine theory to the public.”3
English-language commentators have mostly consigned Serre to the margins and footnotes of broad surveys of harmonic theory. Even though Matthew Shirlaw characterizes Serre’s Essais as “a not unimportant work on harmony,” he devotes only four sentences to a summary description (one might say a summary dismissal) of Serre’s work (1917, 302). Joel Lester cites Serre as a representative example of the “scientifically oriented musical amateurs” whose theoretical speculations were hobbled by “their lack of professional-level musical experience” (1992, 199–200). In a similar vein, Thomas Christensen argues that it is difficult to “make sense” of Serre’s theories (1993, 167n124). Writers in French and German, on the other hand, have been a little more generous in their evaluations of Serre. The Swiss musicologist Erwin Jacobi notes that Serre’s intermediate position between the theories of Rameau and Tartini drew favorable attention from Jean-Jacques Rousseau (Serre’s contemporary and fellow Genevan) and played an important role in eighteenth-century debates on music theory.4 The French composer Lucien Chevaillier went even further, calling Serre “one of the most penetrating and significant minds of his time with regard to musical matters.”5 A re-evaluation of Serre’s theories may thus be overdue.
This article examines aspects of Serre’s harmonic theories, focusing on the second and third of the three Essais from 1753. The second essay sets forth Serre’s treatment of what he calls the “essentially fundamental bass (basse essentiellement fondamentale), as distinguished from the fundamental bass of Rameau. Serre’s third essay focuses on the derivation of the minor mode using two different methods. As noted by Chevaillier and Jacobi, Serre’s harmonic theories shared elements with those of his contemporaries, such as Rameau, Tartini, and Johann Philipp Kirnberger, often charting a middle course between them. Serre’s identification of the tonic, subdominant, and dominant triads as the only possible fundamental harmonies in the major mode arguably presents an early form of function theory, while his use of dual fundamentals reveals interesting connections to the theories of his contemporaries and prefigures theories of mixed harmonic function put forward by modern-day scholars such as Kevin Swinden. In addition, Serre’s theories of the derivation of the minor mode and the dualistic qualities of inversionally related progressions are based on the same principles that would later form the basis of the dualistic theories of nineteenth-century figures such as Moritz Hauptmann, Arthur von Oettingen, and Hugo Riemann. I would argue that Serre’s theories therefore merit more than the passing interest that they have been accorded in English-language scholarship.
1. The Essentially Fundamental Bass
For Serre, as for Rameau, the primary object of music theory is the study of harmony, especially the fundamental bass.6 In particular, Serre states that it is important for a theorist to understand the different fundamental progressions that are possible before trying to explain the physical and mathematical laws underlying these progressions.
Serre begins by acknowledging the pioneering contributions made by Rameau towards the study of fundamental bass progressions in Traité de l’harmonie (1722) and Génération harmonique (1737). Serre argues, however, that Rameau’s fundamental bass is a bit of a misnomer: “however useful, convenient, or analogous it may be to [musical] practice, it is in many cases more of a guiding or methodical bass, rather than a true progression of fundamental sounds of harmony and modulation” (italics added).7 In effect, Serre accuses Rameau of being too much of a practical theorist, and not enough of a speculative one. Rameau’s theory famously “attempt[s] to ground music in a ‘natural principle’” (Cohen 2001, 68). In Serre’s view, however, Rameau is too willing to accept exceptions and contradictions that are dictated by practice, resulting in a method that “subordinates . . . Science to Art, Calculation to Temperament, in a word, Theory to Practice.”8 Serre claims that a true theory of music should not be subject to the whims of practice. In the realm of theory, one must not confuse a “convenient hypothesis” with the “true System of Nature.”9
Serre’s “essentially fundamental” bass (basse essentiellement fondamentale) is designed to correct what Serre perceives to be the shortcomings of Rameau’s “methodically fundamental” bass (basse méthodiquement fondamentale). In Serre’s system, the only fundamental harmonies are those that can be derived from the principle of resonance, i.e., from the overtone series. In other words, only major triads can be fundamental harmonies. In the key of C major, therefore, the only fundamental tones are C, G, and F, and the only fundamental harmonies are the tonic, dominant, and subdominant triads built on those fundamental tones.10 Only a progression containing exclusively tonic, dominant, and subdominant harmonies in the major mode can constitute a rigorously fundamental progression that is susceptible to physical and mathematic proof (Serre 1753, 38). Serre’s view of the tonic, dominant, and subdominant chords as foundational within a key and his narrowing of permissible fundamentals to that group of three can be considered an early form of functional theory that arguably anticipates the three-function harmonic theories of Riemann and other nineteenth-century theorists, even though Serre’s concept of the three harmonic functions does not carry syntactical (or progressional) implications.
2. Fundamental Tones of Non-Triadic Chords
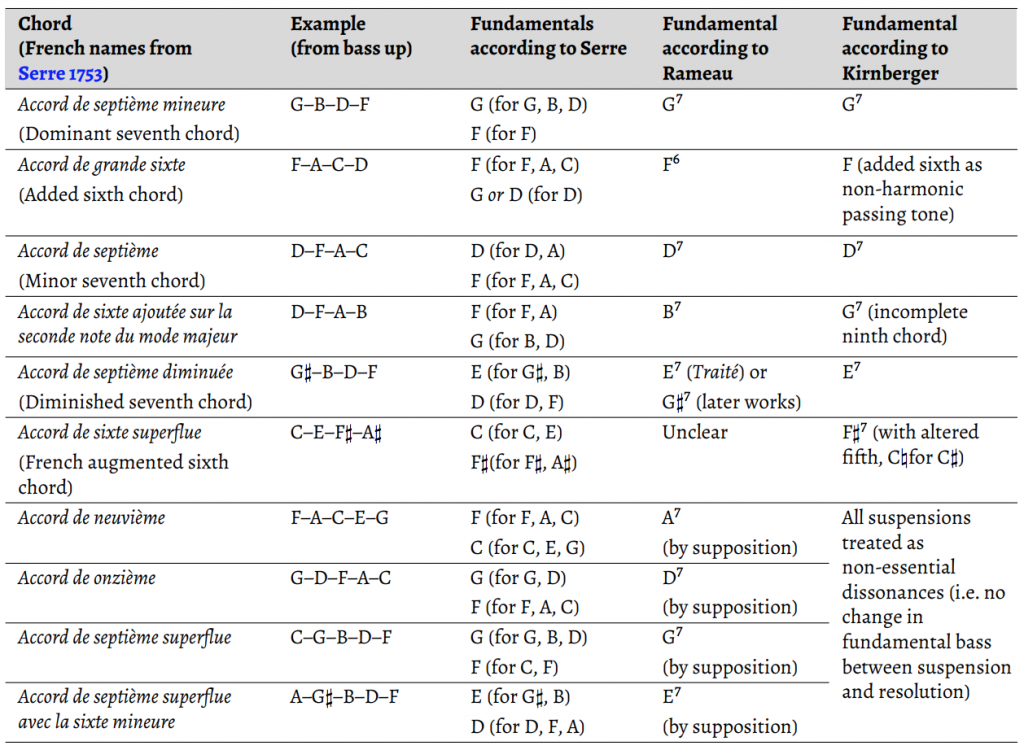
Unlike in the theories of Rameau (and later of Kirnberger), four-note chords are not fundamental harmonies for Serre, since they cannot be derived from the overtone series of a single fundamental tone. Serre’s solution to this problem is to assign dual fundamentals to seventh chords and other chords with four or more tones.
Table 1 summarizes the fundamentals assigned by Serre to various chords and compares them with the fundamentals that would be assigned to the same chords by Rameau and Kirnberger.11 Serre’s dual fundamentals coincide with (or differ from) Rameau’s and Kirnberger’s single fundamentals as discussed below.
2.1 Dominant seventh chords.
Serre points out that in a “chord of the minor seventh” (i.e., a dominant seventh chord) such as G–B–D–F, the lower note in the interval of the minor seventh (G) is not the fundamental of the higher note (F) from an acoustical perspective. Rather than deriving F as an approximation of the seventh partial of G, Serre argues that it would make more sense to derive G as the ninth partial, or the second-order member of Rameau’s “triple progression” (32 = 9), from a lower fundamental of F.12 According to Serre, the apparent interval of the minor seventh G–F (represented by the ratio 9:16) is actually an inversion of the major ninth or major second F–G (1:9 or 8:9). When the entire chord of the minor seventh is inverted into the chord of the tritone, or F–G–B–D (1:9:27:45), we can clearly see from the ratios that F is not generated by a fundamental of G; if anything, it is G that is (distantly) generated by a fundamental of F.13 Accordingly, whereas Rameau assigns G as the single fundamental of the chord G–B–D–F, Serre argues that the chord actually has two fundamentals: G and F.
Serre’s derivation of the dominant seventh chord is thus different from Rameau’s. In Rameau, “the seventh is the origin of all dissonances, [and] the seventh chord is the origin of all dissonant chords” ([1722] 1971, 114). In Serre’s view, however, the minor seventh G–F in the chord G–B–D–F is simply an inversion of the major second that separates the dual fundamentals of the subdominant (F) and the dominant (G). The fact that F happens to form a minor third above D (the fifth of the G major triad) is coincidental and beside the point.14 Serre thus rejects Rameau’s view that seventh chords are formed by stacking thirds above triads.
2.2 Subdominant added sixth and supertonic seventh chords
For Rameau’s added sixth chord F–A–C–D (Serre calls it “l’accord de grande sixte,” or chord of the major sixth), Serre assigns the two fundamentals F (for F, A, and C) and either G or D (for D). Since only major triads can be fundamental harmonies in Serre’s system, a D fundamental necessarily implies a modulation from C major to G major, with D major functioning as the dominant of G major. In order to avoid the implication of modulation, Serre prefers to use F and G as fundamentals for the added sixth chord rather than F and D.15
When the added sixth chord is inverted into the supertonic seventh chord D–F–A–C, however, Serre argues that since D is now the lowest tone in the chord, it is difficult to avoid hearing D as the fundamental for both itself and its upper fifth A. The note A is thus doubly determined in the chord: it is both the fifth of D and the major third of F (Serre 1753, 59–60).
There are two interesting points to note in Serre’s discussion of the added sixth chord. First, he regards the added sixth position of the chord ( $$6 \atop 5$$ in figured bass) as the “direct” position and the root-position seventh chord itself as an “inversion.” This reinforces the notion that Serre does not assign priority to stacks of thirds. Second, different fundamentals can be assigned to different inversion of the same chord: F and G for F–A–C–D, compared to F and D for D–F–A–C. In concept, if not in practice, this is reminiscent of Rameau’s assignment of two different fundamentals (through the use of double emploi) to those same inversions.
2.3 Leading-Tone Seventh Chords
The leading-tone seventh chord in major (viiø7), e.g., B–D–F–A in C major, has the same fundamental tones as the dominant seventh and added sixth chords, namely the dominant (G) and the subdominant (F). Similarly, the leading-tone seventh chord in minor (viio7), e.g., G\sharp–B–D–F in A minor, is built on the dominant (E) and subdominant (D) of the minor mode.16 In comparison, Rameau’s view of the diminished seventh chord changed over time. In the Traité, Rameau assigned a “borrowed” dominant fundamental to leading-tone seventh chords, with $$ \hat6 $$ substituting for the missing $$ \hat5 $$ ([1722] 1971, 93–95). In later writings such as the Code de musique pratique (1760), however, Rameau treated the leading tone itself as the fundamental for leading-tone seventh chords. Serre explicitly rejects Rameau’s later formulation, noting that leading-tone chords can always be generated (at least in part) by a dominant fundamental.17
2.4 Augmented sixth chords
Serre gives as an example of the augmented sixth chord the French augmented sixth chord in E minor, or C–E–F$$\sharp$$–A$$\sharp$$. The dual fundamentals for this chord are C and F$$\sharp$$, or $$ \hat6 $$ and $$ \hat2 $$ in E minor. This seems problematic, since the assigned fundamentals do not function as either subdominant or dominant in the key of E minor, but Serre does not identify or address this as a problem.
Serre’s assignment of $$ \hat2 $$ as a fundamental for the augmented sixth chord is consistent with the views of Kirnberger and later theorists up to Schoenberg, and readily explains the resolution of the augmented sixth chord into a dominant chord through a falling fifth in the fundamental bass (F$$\sharp$$–B in our E minor example). However, instead of discussing the resolution of the augmented sixth chord (fundamental of F$$\sharp$$ resolving to B by descending fifth), Serre (1753, 60–61) focuses on how the chord can be approached from the chord of the relative major, G major (alternate fundamental of C approached from G by descending fifth). A comparison with Rameau is difficult in this case since “Rameau had particular troubles with [the augmented sixth chord], being unable to explain its origin by any of his usual methods” (Harrison 1995, 172n4).
2.5 Chords by supposition
Serre’s approach to chords by supposition differs from Rameau’s. For example, in Rameau, the incomplete (or heteroclite) eleventh chord G–D–F–A–C has a fundamental bass of D7, with G (a perfect fifth below the fundamental bass) acting only as the bass by supposition.18 Serre (1753, 62), on the other hand, treats this and other five-note chords exactly the same as seventh chords, tracing each note in the chord to a fundamental generating tone. In the case of the eleventh chord, the dual fundamental tones are, once again, the dominant G (generating G and its upper fifth D), and the subdominant F (generating the triad F–A–C). In contrast with both Serre and Rameau, Kirnberger treats ninths and elevenths as suspensions or non-essential dissonances in a way that will be familiar to modern theorists and does not assign a separate fundamental bass to suspensions and chords of resolution ([1773] 1979, 178–182).
2.6 Evaluation
As Lester has noted, Serre’s essentially fundamental bass method “yields multiple [fundamentals] for many chords, often including notes absent from the chord themselves” (1992, 200). Even though that might appear like an odd conceit at first, it is arguably no stranger than other theoretical fictions created by fundamental bass theorists throughout the eighteenth and nineteenth centuries, starting with Rameau himself. As noted above, Rameau’s use of double emploi provided a rough precedent for Serre’s practice of assigning different fundamentals to the subdominant added sixth and supertonic seventh chords. Tartini, with whose work Serre was well acquainted, assigned multiple fundamentals to minor triads (ibid., 197–199). Rameau’s use of supposition to imagine alternate basses for a given vertical sonority and Simon Sechter’s later use of concealed fundamentals to explain “impermissible” fundamental-bass progressions are other examples of theorists creatively assigning unobvious fundamentals to chords and progressions.19 Serre’s work thus fits fairly well into this speculative tradition of fundamental-bass theory.
3. Fundamental Successions: A Comparative Analysis
We will now consider how Serre’s theory of the essentially fundamental bass works in practice. Figure 1 is a reproduction of Planche (Plate) I from Serre’s Essais. The figure shows analyses of the same chord progression using the different fundamental-bass theories of Rameau and Serre. The three staves grouped together as System A are taken from Example 23 of Rameau’s Génération harmonique, transposed down a fifth by Serre to C major from Rameau’s original G major.20 The upper two staves feature a chord progression with a figured continuo bass. The third staff of System A shows Rameau’s fundamental-bass analysis of the progression.
I have added measure numbers above the topmost staff (including for the first and last partial measures) for ease of reference in the ensuing discussion. Since the progression involves the use of suspensions, I will also discuss Kirnberger’s treatment of suspensions as non-essential dissonances as an additional comparison to the theories of both Serre and Rameau.
System B shows Serre’s fundamental-bass analysis of this progression, with the fundamental tones expressed as members of the triple progression over the subdominant F (Fa) (1), with C (Ut) expressed as a fifth above F (31 = 3), G (Sol) as two fifths above (32 = 9), and D as three fifths above (33 = 27).21 Dual fundamentals are shown as two numerals, one above the other. System C expresses the same information as System B, but with the fundamentals expressed as notes on a bass clef. In the two staves of System D, the dual fundamentals are split into two lines, with the upper progression labeled the “superior” progression and the lower succession labeled the “inferior” or “contrabass” progression. In the explanatory text to this figure, Serre calls the “superior” line of System D the “dominant” progression, and the “inferior” line the “subdominant” progression (1753, 101). Finally, in System E, Serre picks one of each pair of dual fundamentals as the principal fundamental (basse fondamentale prédominante). The principal fundamentals remain as noteheads, while the secondary fundamentals are now shown by a symbol called a “guidon,” which resembles the letter w.22 Although Serre does not give any explicit guidelines or preference rules to explain how he has selected a principal fundamental from a pair of candidates, his choice for principal fundamental in each case is the note that generates the greatest number of notes in the chord, with only one exception (the first chord in m. 7).23
How do the parallel analyses of Rameau and Serre differ from each other? The chord progression shown in Figure 1 starts with a C-major tonic chord and returns to the tonic three times (in mm. 2, 4, and 8). In mm. 1–2, the two tonic chords are separated by a dominant seventh chord, with a tonic pedal in the continuo bass. Rameau’s fundamental bass for these three chords is C–G7–C. In the text discussing this example in Génération harmonique, Rameau explains that the sounding bass note C in the first chord of m. 2 is treated as a bass by supposition, a fifth below the fundamental bass of G (1737, 160). In other words, Rameau treats the chord C–G–B–D–F as a heteroclite eleventh chord. Serre’s essentially fundamental bass for the same chords is C–[F/G]–C (see Systems B through D), with C–G–C constituting the principal fundamental bass (System E).24 Serre’s principal fundamental bass is thus outwardly similar to Rameau’s. However, we should note that in Serre’s reading, the tonic pedal C in the first chord of m. 2 is generated as the upper fifth of the co-fundamental F, rather than as the lower fifth of Rameau’s fundamental G.
In mm. 3–4, a major ninth chord over F in the bass leads first to an added sixth chord over the same bass before moving to a dominant seventh chord over G, and finally to the tonic triad. For Rameau, the fundamental bass of the ninth chord on the downbeat of m. 3 is A7, with the actual bass tone derived by supposition as a major third below the fundamental bass (see the third staff in System A). Within this context, Rameau reads the second chord of m. 3 as an inversion of a supertonic seventh chord with a fundamental bass of D7, rather than as a subdominant added sixth chord. This reading allows Rameau to create a chain of dominants leading to the tonic in m. 4, with a fundamental bass descending by perfect fifths. Rameau’s “mechanistic” model of harmonic motion driven by successive resolutions of the fundamental dissonance of the seventh is neatly illustrated in his analysis of these two measures.25
Serre’s analysis of mm. 3–4 is completely different from Rameau’s. In contrast to Rameau’s falling fifths in the fundamental bass (A7–D7–G–C), Serre’s essentially fundamental bass for these four chords is [F/C]–[F/G]–[F/G]–C. One of the anomalies in Serre’s analysis is that the dual fundamentals for the second chord in m. 3 (supertonic seventh or subdominant added sixth) and the first chord in m. 4 (dominant seventh) are the same. Joel Lester reads Serre’s analysis as implying that “there is no harmonic progression” from ii7–V7 in C major (1992, 200).
While Lester’s point is well taken, Serre appears to be at least somewhat sensitive to this problem. In the principal fundamental bass for mm. 3–4 shown in System E (F–F–G–C), Serre actually does show a change in fundamental from F to G across the barline into m. 4. In the analysis in System E, Serre in effect reads the two chords in m. 3 as having subdominant function, and the two chords in m. 4 as having dominant and tonic function, respectively. One could perhaps argue further that the allocation of the same principal fundamental to both chords in m. 3 hints obliquely at Kirnberger’s distinction between essential and non-essential dissonances.26 The ninth and seventh above the bassin the first chord of m. 3 (G and E) are non-essential (or suspended) dissonances in Kirnberger’s formulation that resolve to an octave and a sixth above the bass (F and D) in the next chord. Kirnberger would thus have assigned the same fundamental to both chords in m. 3, much as Serre does in System E. Serre’s principal fundamental analysis of m. 3 thus has “Kirnberger-like” overtones, although a Kirnberger analysis of m. 3 would probably show a fundamental of D7 instead of Serre’s F.27 In any event, Serre’s analysis of mm. 3–4 (at least in System E) is perhaps not as musically insensitive and outlandish as Lester makes it out to be. The analogy drawn here between Serre and Kirnberger must be qualified, however, by the recognition that Kirnberger’s analytical examples (and the theory underlying them) are much more lucidly and consistently worked out than Serre’s.28
Serre’s analysis of mm. 5–6 of Figure 1 is also interesting. In mm. 5–6, the right-hand part is identical to mm. 3–4: the only change is that the left hand plays D in both chords in m. 5, compared to F in m. 3. This change has no effect on Rameau’s fundamental-bass analysis: as in mm. 3–4, Rameau shows a chain of falling fifths in the fundamental bass (A7–D7–G7–C), with the first chord of m. 5 treated, like the corresponding chord in m. 3, as a chord by supposition, with an actual bass that is a fifth below the fundamental (compared to a major third below the fundamental in the first chord of m. 3).29 Kirnberger would probably also have kept the same fundamental bass (in his case, D7) for mm. 3 and 5: in both measures, G and E constitute non-essential dissonances that resolve to F and D in a supertonic seventh chord.30
In contrast to Rameau and Kirnberger, the change in bass tone from F in m. 3 to D in m. 5 has a material effect on Serre’s analysis. Serre’s dual fundamentals for the chords in m. 5, as reflected in System C, are [C/D]–[F/D], compared to [F/C]–[F/G] in m. 3. Since there is no F in the first chord of m. 5, Serre is forced to substitute D as a fundamental in order to generate the pitches D and A in that chord (A is generated by F in the corresponding chord in m. 3). When he is then required to choose either C or D as principal fundamental for the first chord in m. 5 in System E, Serre chooses the tonic C. The resulting C–F–G–C fundamental succession in mm. 5–6 resembles a Riemannian cadential progression (T–S–D–T).31
Measures 7–8 of Figure 1 show a perfect authentic cadence with a 4–3 cadential suspension over the dominant in m. 7. Rameau’s fundamental bass for the last three chords is once again a series of descending fifths: D7–G7–C. In the first chord of m. 7, the suspended C is treated as a seventh over the fundamental bass D instead of a fourth over the actual bass G. That actual bass G is derived by supposition as a fifth below D. In contrast to Rameau, Kirnberger would likely have assigned G7 as the fundamental for both chords in m. 7, with the C treated as a suspended non-essential dissonance.
Serre’s analysis is once again different from those of Rameau and Kirnberger. In System C, Serre gives a fundamental succession of [C/G]–[F/G]–C for mm. 7–8, from which he extrapolates a principal succession in System E of C–G–C.32 As in m. 5, the first chord in m. 7 is assigned a tonic fundamental, even though the only note that suggests tonic in m. 7, the C in the soprano, is actually a suspended dissonance. Serre’s analysis of the cadential suspension in m. 7 is puzzlingly inconsistent with his arguably more musical analysis of the similar suspension in m. 3.33
4. Fundamental Tones of the Minor Triad
In the third of the Essais, Serre turns his attention to the minor mode. In the first part of the essay, Serre discusses two alternative methods of assigning fundamental tones to the minor triad A–C–E. The first alternative is to consider the three notes A–C–E as overtones of an omitted lower fundamental F.34 Since E is a rather distant partial of F, this does not seem like the best solution. We should note, however, that F is actually one of the two roots assigned to the A-minor triad by Tartini, with whose theoretical work Serre was well acquainted. Tartini uses the “third sound” (terzo suono), or first-order difference tones, of chords as the root(s). In the case of the minor triad, Tartini assigns multiple roots. For the A-minor triad in root position, Tartini’s roots would be F and C.35
Serre’s second alternative is to consider A and C as dual fundamentals of the A-minor triad, with E simultaneously constituting the fifth of A and the major third of C. The reasoning behind this second alternative is clearly influenced by Rameau’s discussion of the co-generation of the minor triad in the Démonstration du principe de l’harmonie (1750), an influence that is acknowledged by Serre.36 Serre describes how the mode of A minor can be understood to involve a “very fortunate complication” (une complication très-heureuse) with the mode of C major, with A minor constituting the principal mode, and C major the “subaltern” mode (1753, 126–127). The relative minor and major modes together form a “union” or a “harmonic society” (société harmonique), a conceit reminiscent of Rameau’s “grand community of sounds” (grande communauté de sons) formed by the two modes (ibid., 127; Rameau 1750, 72). Serre notes that this union is threatened only at cadential points, where the leading-tone (G$$\sharp$$) of the principal mode (A) takes precedence over the dominant (G$$\natural$$) of the secondary mode (C).
Even though Serre conceives of the minor triad as doubly determined, he endorses Rameau’s practice of assigning a single fundamental to the minor triad as a kind of analytical shorthand, arguing that the secondary fundamental (the third of the minor triad) is implied (1753, 130–131). In practice, therefore, Serre’s fundamental-bass analyses assign only one fundamental to the minor triad, like Rameau (but unlike Tartini). Without the convenience of this analytical shorthand, Serre would need to assign three fundamentals [D/E/F] to the diminished seventh chord (G$$\sharp$$–B–D–F), instead of the two fundamentals [D/E] discussed above in Table 1. However, the arbitrary omission of certain fundamentals in a system that explicitly provides for multiple fundamentals makes for a somewhat confusing and inconsistent state of affairs; perhaps this is unavoidable in any theory that seeks to explain the minor mode using the overtone series.
5. Serre the Dualist
Having first discussed the minor triad and its fundamental tones according to what he terms the ‘principle of resonance,’ Serre sets forth an alternative view of the minor mode in the final part of the Essais. Here, the minor mode is conceived as the dualistic inverse of the major mode. In order to illustrate this dualistic view of the minor mode, Serre first sets aside the principle of resonance, which is based on the acoustical properties of a sounding body (corps sonore), and considers instead the “principle of ratios,” under which pitches are designated as integers or fractions, and pitch relations are designated as ratios.37
For the C-major scale, Serre assigns the following integers, with the lowest pitch F assigned the number 1:
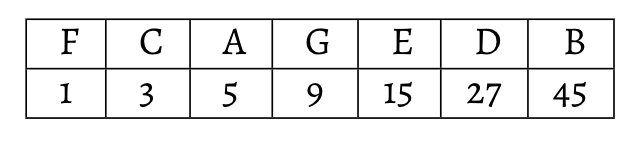
Pitches related to each other through the circle of fifths are related by ratios of the triple progression (F:C = 1:3, F:G = 1:9, A:E = 5:15, etc.), while pitches separated by a major third are related by ratios of the quintuple progression (F:A = 1:5, C:E = 3:15, G:B = 9:45).
Serre notes that the same pitches can be rearranged and expressed as inverses of the integers shown above, with the highest pitch B assigned the number 1 and the other pitches represented as fractions thereof:

The position occupied by C in the first set of pitches is occupied by E in the inverse set. From this, Serre concludes that in the same sense that C is considered the tonic of the “direct mode” of C (or C major), E can be considered the tonic of the “inverse mode” of E (or E Phrygian).
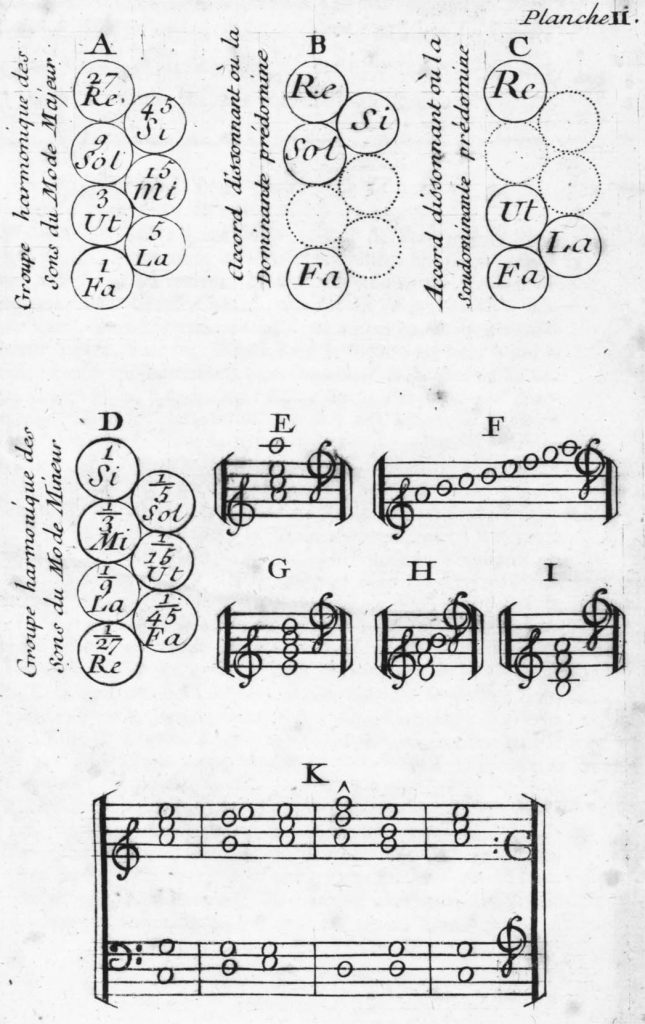
Figure 2, a reproduction of Planche II from the Essais, shows Serre’s diagrammatic depictions of these inverse relations. Diagram A in Figure 2 is a Tonnetz-like depiction of the pitches of the C-major mode, with fifth-related pitches forming the vertical axes and major-third-related pitches forming the diagonal axes. The three primary triads are represented by three triangular clusters of pitches, with the tonic triad (C–E–G, or Ut–Mi–Sol) in the center, flanked by the dominant triad above and the subdominant triad below. Diagrams B and C illustrate the complementary positions occupied by the dominant seventh chord (Diagram B) and the subdominant added sixth (or supertonic seventh) chord (Diagram C) in this space.
Diagram D represents the inverse of Diagram A. We can see that the central triad, i.e., the triad that corresponds to C–E–G (Ut–Mi–Sol, reading up) in Diagram A, is E–C–A (Mi–Ut–La, reading down) in Diagram D. Thus, the A-minor triad (generated downward from E) is in this sense the inverse of the C-major triad (generated upward from C).
Although Serre does not mention it in his text, the pitch D (Re) forms the axis of inversion between Diagrams A and D, as reflected by the position of Re at the top of Diagram A and the bottom of Diagram D. Serre exploits this property of inversional symmetry in Diagrams E through K. By using a G clef on the bottom line (giving the pitch D on the middle line, as in bass clef), Serre shows how the C-major triad (Diagram E) and the C-major scale (Diagram F) can literally be “flipped over,” or transformed by a “mirror reflection,” into the A-minor triad and the E-Phrygian scale, respectively. Diagram F shows that the position occupied by the tonic C in the major scale is occupied by E in the inverse Phrygian scale. Indeed, Serre calls the dualistically generated Phrygian scale the “inverse mode of E” (Mode inverse de mi). Serre reconciles this inverse mode of E with the A-minor mode by noting that the principle of resonance causes us to perceive the lower note A in the fifth A–E as the tonic, and thus strips E of its tonic status in the inverse mode.38 A further exploration of the special status of E within the A minor mode would have to wait for the later dualistic theories of Moritz Hauptmann and Hugo Riemann.39
Diagrams G through I show mirror images of common chords, while Diagram K shows a progression in C major that, when reflected in a mirror or read upside down, becomes a progression in A minor.40 In the case of the “reflected” or “inverse” diagrams, Serre asks the reader to mentally raise G to G\sharp where a leading tone in A minor is required.41 Serre further notes that by changing the clef and providing different sets of accidentals, the diagrams in Figure 2 can be generalized to cover all the major and minor keys.
Table 2 summarizes the inversional properties illustrated by Figure 2. As we can see from the table, the authentic cadence (of sorts) shown in Diagram K becomes a quasi-plagal cadence in the inverse mode. In other words, the dualistic modes generate dualistic (or inversional) harmonic functions. Serre’s exploration of the dualistic properties of the major and minor modes, which was possibly inspired by Rameau’s exploration of the inversional properties of the dominant seventh and subdominant added sixth chords in Génération harmonique, predate Arthur von Oettingen’s exploration of harmonic dualism in Harmoniesystem in dualer Entwickelung (1866) by more than a hundred years. Fascinatingly, like Serre before him, Oettingen would also intentionally use the bass clef (with D on the middle line) in order to explore notational symmetries.42 Indeed, the inversionally related cadential progressions in Figure 3, reproduced from Oettingen’s treatise, bear a distinct resemblance to Serre’s Diagram K.43 If we are to agree with Daniel Harrison that Oettingen’s later work on the mirror-image properties of the major and minor modes “offer[s] insights of considerable artistic and theoretical value” (1994, 250), then we should not forget the pioneering efforts of Serre in this regard.
6. Reception and Evaluation
Serre occupies a marginal position in the history of theory, and as I noted in the introduction to this article, contemporary commentators in English have been less than kind in their assessment of his theory of the essentially fundamental bass. Lester (1992, 200) cites Serre’s analysis in Figure 1 as a prime example of the “absurdities” that abound in works by eighteenth-century musical amateurs, even as he acknowledges that amateurs like Serre were taken seriously by musician-theorists of the day. Christensen argues that “[e]ven disregarding the question of how a musician is to make sense of a double or triple root, Serre’s theory would make utterly useless the various species of fundamental bass motion Rameau identifies, since he provides no criteria by which one may prioritize the various roots” (1993, 167n124).
As Lester and Christensen correctly point out, Serre did not fully develop a practicable system of analysis base on his theory of the essentially fundamental bass. To critique Serre’s theories in this manner, however, is to privilege practical application over theoretical speculation, in a question of how a musician is to make sense of a double or triple root, Serre’s theory would make utterly useless the various species of fundamental bass motion Rameau identifies, since he provides no criteria by which one may prioritize the various roots” (1993, 167n124). As Lester and Christensen correctly point out, Serre did not fully develop a practicable system of analysis based on his theory of the essentially fundamental bass. To critique Serre’s theories in this manner, however, is to privilege practical application over theoretical speculation, in a spirit that is contrary to Serre’s stated intent. Serre’s work, viewed in its own right, serves as an illuminating illustration of the ways in which speculative thinkers (including musical amateurs not bound by the strictures of practice) tried to understand and systematize musical thought in the eighteenth century. An examination of Serre’s essays also reveals that fundamental-bass theory was not a monolithic theory, but one whose application was in constant flux even among its adherents. Serre’s isolation of the tonic, subdominant, and dominant triads as foundational harmonies prefigures nineteenth-century theories of harmonic function, and his idea of dual fundamentals addresses important and persistent questions regarding “mixed” chords. These issues have engaged theorists from different eras: Rameau himself recognized the mixed dominant/subdominant derivation of the dominant seventh, added sixth, and diminished seventh chords in Génération harmonique, and the notion of chords with mixed derivation and/or mixed function persists from the work of Hauptmann and Riemann to that of present-day scholars such as Harrison and Swinden.44
Serre’s pioneering work on harmonic dualism is even less well known and examined than his work on the essentially fundamental bass. Theories of harmonic dualism are most often credited to nineteenth-century German theorists in historical surveys: Harrison’s (1994, 215–218) influential account of the history of these theories charts a line from Hauptmann to Hermann von Helmholtz, Oettingen, and Riemann (while acknowledging that these theories can be traced ultimately to Rameau’s work). In light of the wide-ranging scholarship on nineteenth-century German theories of dualism in recent decades, it is remarkable that Serre’s exploration of harmonic dualism in the Essais, which preceded the work of those notable German theorists by almost a century, remains so little known. It is difficult to trace a direct line from Serre to the nineteenth-century German dualists, although Serre does rate a very brief mention in Riemann’s history of music theory (1898), in a convoluted footnote that quotes a reference by Rousseau to Serre’s use of mirror images in the Essais.45 And yet one need not trace a line of causality or influence in order to appreciate the significance of Serre’s work on dualism. Serre’s theories productively complicate received historical narratives about both eighteenth-century harmonic theory and nineteenth-century theories of harmonic dualism and harmonic function, revealing that these theories have more complex lineages than the teleological ones often given in broad historical surveys. Serre thus deserves to be more than a footnote in the history of music theory.
Andrew Pau is an Associate Professor of Music Theory at Oberlin College & Conservatory. His research interests include the French Belle Époque, nineteenth-century opera, phrase rhythm and text setting, chromatic harmony, and theories of narrative. Andrew’s work has previously been published in Music Theory Spectrum, Music Theory Online, and Theory and Practice. He is a graduate of the Mannes School of Music (M.M., piano) and the CUNY Graduate Center (Ph.D., music theory).
References
Bernstein, David W. 2002. “Nineteenth-Century Harmonic Theory: The Austro-German Legacy.” In The Cambridge History of Western Music Theory, edited by Thomas Christensen, 778–811. Cambridge: Cambridge University Press.
Boccadoro, Brenno. 1993. “Jean-Adam Serre: un juste milieu entre Rameau et Tartini?” Revue de Musicologie 79 (1): 31–62.
Chevaillier, Lucien. 1925. “Les théories harmoniques.” In Encyclopédie de la musique et Dictionnaire du Conservatoire, edited by Albert Lavignac and Lionel de la Laurencie, Part 2 Vol. 1, 519–590. Paris: Delagrave.
Christensen, Thomas. 1993. Rameau and Musical Thought in the Enlightenment. Cambridge: Cambridge University Press.
Clark, Suzannah. 2001. “Seduced by Notation: Oettingen’s Topography of the Major-Minor System.” In Music Theory and Natural Order from the Renaissance to the Early Twentieth Century, edited by Suzannah Clark and Alexander Rehding, 161–180. Cambridge: Cambridge University Press.
Cohen, David. 2001. “ ‘The Gift of Nature’: Musical ‘Instinct’ and Musical Cognition in Rameau.” In Music Theory and Natural Order from the Renaissance to the Early Twentieth Century, edited by Suzannah Clark and Alexander Rehding, 68–92. Cambridge: Cambridge University Press.
Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. Chicago: University of Chicago Press.
———. 1995. “Supplement to the Theory of Augmented-Sixth Chords.” Music Theory Spectrum 17 (2): 170–195.
Hauptmann, Moritz. (1853) 1991. The Nature of Harmony and Metre. Translated and edited by W. E. Heathcote. Reprint, New York: Da Capo Press.
Jacobi, Erwin. 1958. “Jean-Adam Serre, ein vergessener Schweizer Musiktheoretiker.” Schweizerische Musikzeitung 98: 145–148.
Johnson, Russell William. 1994. “Essais sur les principes de l’harmonie by Jean-Adam Serre: An Annotated Translation.” M.M. thesis, Florida State University.
Kirnberger, Johann Philipp. (1773) 1979. “The True Principles for the Practice of Harmony.” Translated by David W. Beach and Jürgen Thym. Journal of Music Theory 23 (2): 163–225.
Lester, Joel. 1992. Compositional Theory in the Eighteenth Century. Cambridge: Harvard University Press.
Oettingen, Arthur von. 1866. Harmoniesystem in dualer Entwickelung: Studien zur Theorie der Musik. Dorpat and Leipzig: W. Glaser.
Rameau, Jean-Philippe. (1722) 1971. Treatise on Harmony. Translated by Philip Gossett. New York: Dover.
———. 1737. Génération harmonique, ou Traité de musique théorique et pratique. Paris: Prault.
———. 1750. Démonstration du principe de l’harmonie, servant de base à tout l’art musical théorique et pratique. Paris: Durand, Pissot.
Riemann, Hugo. 1898. Geschichte der Musiktheorie im IX. – XIX. Jahrhundert. Leipzig: Max Hesse.
Rousseau, Jean-Jacques. 1768.Dictionnaire de musique. Paris: Duchesne.
Senebier, Jean. 1806. Histoire littéraire de Genève, Vol. 3. Geneva: Manget.
Serre, Jean-Adam. 1753. Essais sur les principes de l’harmonie. Paris: Prault.
———. 1763. Observations sur les principes de l’harmonie. Geneva: Gosse.
Shirlaw, Matthew. 1917. The Theory of Harmony: An Inquiry into the Natural Principles of Harmony, with an Examination of the Chief Systems of Harmony from Rameau to the Present Day. London: Novello.
Swinden, Kevin. 2005. “When Functions Collide: Aspects of Plural Function in Chromatic Music.” Music Theory Spectrum 27 (2): 249–282.
Notes
- Senebier 1806, 326. Erwin Jacobi (1958, 145) notes that there is scant biographical information on Serre beyond brief anecdotes cited in various Genevan and Swiss sources (Geneva joined the Swiss Confederation following the Napoleonic Wars). As a result, there appears to be no readily available information on Serre’s musical background and his interests in music beyond his two publications noted in this paragraph.
- The New Grove Dictionary of Music and Musicians, 2d ed., s.v. “Serre, Jean-Adam.”
- Serre 1753, iii (“L’Expérience témoigne assez combien les Artistes les plus consommés dans leur Art sont peu propres ou peu disposés à en donner au Public une véritable Théorie”). Unless otherwise noted, the English translations in this article are my own. For a complete English translation of Serre’s Essais, see Johnson 1994.
- Jacobi 1958, 145. Jacobi’s article charts a brief reception history of Serre’s theories from the eighteenth century to the first half of the twentieth century
- Chevaillier 1925, 550 (“Serre, à coup sûr, fut un des esprits les plus pénétrants de son temps en même temps que les plus larges, en ce qui concerne les choses musicales”). Chevaillier’s evaluation of Serre is cited approvingly in Boccadoro (1993, 61).
- Serre 1753, 29 (“l’Harmonie est sans contredit le premier objet de la Théorie de la Musique, et particulièrement celui de la Basse fondamentale”). Serre contrasts his harmony-centric approach with the melody-centric approach of his contemporary, the French theorist Charles Henri de Blainville (1711–1769).
- Ibid., 34–35 (“Quelque utile, quelque commode, quelque analogue qu’elle puisse être à la Pratique, c’est plutôt en plusieurs cas une Basse directrice ou méthodique, que la vraie Succession des Sons fondamentaux de l’Harmonie et de la Modulation”).
- Ibid., 50 (“[Rameau a] suivi . . . la Méthode . . . de subordonner dans un grand nombre de cas la Science à l’Art, le Calcul au Tempérament, en un mot, la Théorie à la Pratique”).
- Ibid., 37 (“[O]n est en droit, lorsqu’il s’agit de Théorie, de ne pas confondre l’hypothèse commode, qui s’y trouve sujette, avec le vrai Systême de la Nature”).
- Ibid., 52. Serre uses the term dominante-tonique to refer to the dominant triad. See, e.g., ibid., 38. It is clear from the context, however, that he is not referring to Rameau’s dominante-tonique, or the dominant seventh chord.
- In Table 1, the figure 7 refers to seventh chords, while the figure 6 refers to added sixth chords.
- Rameau (1737) discusses the triple progression in Chapter 4, 42–46.
- Serre 1753, 55–56 (“le fa, [1, 2, 4 ou 8] est bien plutôt Son fondamental et générateur de sol [9], que ce sol ne l’est de fa [16]”).
- Ibid., 58 (“C’est donc essentiellement la Soudominante qu’on ajoute à la Dominante, et non pas une Tierce qu’on place au-dessus de la Quinte de cette Dominante”).
- Ibid., 59. Notwithstanding the reference to modulation here, Serre does not present a comprehensive theory of modulation in the Essais.
- Serre’s dual fundamentals for the diminished seventh chord can be compared with Rameau’s characterization of that chord as combining elements of the dominant and subdominant triads in the minor mode (Rameau 1737, 151). However, there is an important inconsistency in Serre’s treatment of the diminished seventh chord, as the F in the example chord cannot be generated acoustically from either E or D. As discussed below under “Fundamental Tones of the Minor Triad,” Serre conceived of the minor triad D–F–A as doubly determined, with two fundamentals D and F both generating the third note A. However, he endorses the practice of assigning a single fundamental to the minor triad (D in this case) as a kind of analytical shorthand. See Section 4 below. Serre appears to resort to this shorthand here to avoid having to assign a triple fundamental [D/E/F] to the diminished seventh chord.
- Serre 1753, 63–65. Serre’s thoughts on the unsuitability of the leading tone as a fundamental are contained in a discussion on the apparent fundamental progression F–B, which Serre rejects in favor of the progression F–G, arguing that the F–B fundamental succession is only suitable in the case of an abrupt modulation (presumably to a key in which B functions as tonic, dominant, or subdominant).
- Rameau [1722] 1971, 89–91. Rameau’s actual example for this chord is D–A–C–E–G, but I have transposed Rameau’s example down a fifth to correspond with Serre’s example for the same chord.
- For a discussion of Sechter’s fundamental-bass theories, see Bernstein 2002, 788–791.
- In order to avoid confusion with letter names for pitches, I have used bold italics for letters representing the diagrams in the figures.
- Serre observes elsewhere in the Essais that if the tones of the C-major scale are arranged in a chain of perfect fifths (i.e., according to a triple progression), the lowest tone in the chain is the subdominant, F. Serre 1753, 52–53 (“La soudominante fa… est naturellement et essentiellement le Son… le plus grave des sept Sons de la Gamme ut, re, mi, fa, et cetera”). This is the underlying principle behind the numbers used in System B.
- A guidon, in both French and English, is a small military flag used as a unit marker.
- Serre’s indifference to preference rules is reflected in his charmingly offhand remark that “when either of the two possible fundamental tones can appear to dominate equally, we will indifferently write down [as principal fundamental] the one that we want, and mark the other one with a guidon.” Serre 1753, 101. (“Lorsque deux sons fondamentaux pourront paraître dominer également, on notera indifféremment celui qu’on voudra, en marquant l’autre avec un Guidon”).
- Where Serre shows two fundamentals for a chord, I have enclosed both fundamentals in square brackets and separated them with a slash, e.g., [F/G].
- For a discussion of Rameau’s use of mechanistic analogies, see Christensen 1993, 103–132.
- See Kirnberger [1773] 1979, 171–182 (text and accompanying examples).
- Kirnberger generally treats the subdominant added sixth chord as an inversion of the supertonic seventh chord. See, e.g., ibid., 184, Example 15 (first chord).
- As discussed below, for instance, Serre does not treat the suspended dissonances in mm. 3 and 7 of Figure 1 in a consistent manner.
- The figure 7, which should be above the fundamental bass in both chords in m. 5 and the first chord in m. 6 in System A, is omitted (presumably due to a printing error) both in Rameau’s original and in Serre’s adaptation thereof.
- In m. 3, the figures for the non-essential dissonances G and E are 9 and 7 above the continuo bass F (Rameau’s figures omit the 7). In m. 5, the figures for the non-essential dissonances G and E are 11 (or 4) and 9, as reflected in Rameau’s figures.
- Serre’s choice of C as fundamental may reflect the fact that from a “democratic” perspective, the three members of the C major triad (C–E–G) in the first chord of m. 5 outnumber the two members of the D minor triad (D and A). With respect to the fundamental succession C–F–G–C, we should note that unlike Rameau, Serre explicitly allows the fundamental bass to ascend by step from subdominant to dominant, calling it “a very legitimate progression from one fundamental sound to another fundamental sound in the same mode” (1753, 67).
- As noted above, the principal fundamental of each chord shown in System E is generally the fundamental which generates the greatest number of notes in the chord. A tie results when this method is applied to the first chord in m. 7: C generates C–G–G, while G generates G–G–D. Serre does not give any tie-breaking reason for picking C.
- On a humorous side note, Serre’s treatment of the suspension in m. 7 should be frustratingly familiar to generations of music theory teachers who have told their students that the cadential $$6 \atop 4$$ (or the “cadential $$5 \atop 4$$ ” in Serre’s example) is not a tonic harmony.
- Serre 1753, 129–130. In a footnote, Serre acknowledges that even if one considers F the primary fundamental for the triad A–C–E, C can be considered a secondary, weaker fundamental. Ibid., note (u). The pair of fundamentals thus derived (F and C) is identical to the pair postulated for the same chord by Tartini.
- Lester (1992, 197–200) has pointed out that Tartini’s examples contain numerous errors. Serre’s Observations sur les principes de l’harmonie (1763) contains a critique of various aspects of Tartini’s theoretical writings, as well as those of d’Alembert and Geminiani.
- For Rameau’s theory on the minor mode around this time, see Rameau 1750, 62–84.
- Serre 1753, 131. Rameau had inaccurately posited an acoustical basis for his dualistic view of the major and minor triads in Génération harmonique. This scientifically erroneous view was retracted by Rameau in Démonstration. Serre’s Essais were published three years after Démonstration.
- Ibid., 136 (“C’est ce Principe [de la Resonnance] qui modifie l’effet musical des Rapports des Sons, en nous faisant sentir la relation physique qui existe entre eux comme, par exemple, entre les deux Sons qui forment la Quinte de la à mi, dans le Mode inverse, et qui donnant au Son grave la, la qualité de Son fondamental, dépouille en même temps mi du titre de Son principal, de Note tonique…”).
- Hauptmann ([1853] 1991, 14–15) characterizes C in the C-major triad as a “positive unity” that has a fifth and a third (G and E, respectively), and E in the A-minor mode as a “negative unity” that is a fifth and a third (of A and C, respectively). Riemann treats E as the prime of the downward-generated A-minor triad.
- In addition to the G clef on the bottom line, Serre uses the bass clef in Diagram K as well. Both of these clefs show D on the middle line.
- Serre 1753, 140 (“on renverse le Livre… en diézant dans le renversement les sol qu’on voudra rendre Notes sensibles”). The caret (ˆ) over the fourth chord in Diagram K serves as a visual reminder to raise G to G$$\sharp$$ .
- See examples in Clark 2001.
- Figure 3 is reproduced from Oettingen (1866, 77) and is also featured in Clark (2001, 171). As shown in the table, Oettingen used the terms “tonic” and “phonic” in place of “major” and “minor.”
- Harrison (1994) presents a dualistic theory of harmonic function in chromatic music, aspects of which are further explored in Swinden (2005).
- On Rousseau’s quote regarding Serre’s exploration of the inversional properties of the major and minor modes, Riemann comments that “there we already have the harmonic mirror images of Oettingen.” Riemann 1898, 471, footnote (“Da haben wir bereits die ‘Spiegelbilder’ der harmonie A. von Oettingens”). The convoluted nature of this reference makes it difficult to conclude, however, that Riemann had any direct knowledge of Serre’s work. The Rousseau quote cited by Riemann is from the entry “Système” in Rousseau’s Dictionnaire de musique (1768, 483).