Holst’s Planets, The Final Frontier: Interplanetary Voyage as Intrapersonal Escape

Táhirih Motazedian
Scott Murphy

Abstract

Interpretations of Gustav Holst’s The Planets traditionally gravitate around assumptions that Holst was depicting Roman mythology, astrological horoscopes, or astronomical science. But there are numerous contradictions problematizing each of these theories, and even an amalgamation of the three does not fully explain the enigmatic features of this work. Our interpretation of The Planets proposes that Holst envisioned this interplanetary voyage as a metaphorical escape from the bustle of society and even from life itself. We form this interpretation by drawing upon biographical information and intertextual references, as well as an analog to proxemics within pitch-class set theory.
View PDF
Return to Volume 36

Keywords and Phrases: Holst, The Planets, pitch-class set theory, proxemics, transformational combination, esoteric narrative

Introduction

Interpretations of Gustav Holst’s The Planets traditionally gravitate around assumptions that Holst was depicting Roman mythology, astrological horoscopes, or astronomical science, as can be readily observed by perusing virtually any program notes or liner notes written about the suite. But there are numerous contradictions problematizing each of these assumptions, and even an amalgamation of the three does not fully explain the enigmatic features of this work. Drawing upon Arthur Seidl’s distinction between “exoteric” and “esoteric” narratives, we have detected beneath the surface of the planetary voyage a different kind of voyage altogether.¹ Combining musicological and theoretical approaches, we present a new interpretation of The Planets: namely that Holst envisioned this interplanetary voyage as a metaphorical escape from the bustle of society, and even from life itself.

We do not attempt to conclusively define the composer’s deliberate intentions, but rather, we proffer a reader-based interpretation based on clues from Holst’s life and music. In doing so, it is useful to distinguish between “writer” and “author” (as delineated by Foucault [1979] and Nehamas [1986]), in which the “writer” is the historical person who created the work, while the “author” is the person who created the work as interpreted by the reader. The “author,” thus, is “produced through an interaction between [reader] and text” (Nehamas 1986, 686). As readers of Holst’s Planets, we use his biographical information as an interpretive filter to guide our reading of his work—much in the same way readers have long used astronomy/astrology/mythology as interpretive filters for guiding their understanding of The Planets. Drawing connections between various factors in his life and works, we construct an interpretation of the journey Holst constructed. And by “Holst,” of course, we refer to the “author” of this journey.

The first section of our essay (Revisiting the Provenance of The Planets) decouples Holst’s compositional impulse from exclusively astrological, mythological, or astronomical origins. The second section (The Journey) proffers an alternate biographical association for the suite—as a metaphor for a retreat into solitude—and portrays this retreat with a short analytical tour through the work grounded in biographical and intertextual observations, touching lightly on a few technical aspects. The final section (Pitch-Class-Set Proxemics) before the conclusion enlists pitch-class set theory and some original forms of measurement within this theory, to propose a more quantified trajectory of this retreat through a succession of characteristic pitch materials through the entire suite.

1. Revisiting the Provenance of The Planets

1.1 Not Strictly Astrological, Mythological, or Astronomical

Astrology, mythology, and astronomy were obviously major influences in Holst’s conception and composition of his Planets, and these three systems have a long history of overlapping with and influencing one another. But Holst did not adhere exclusively to the tenets of any one of these systems, rather, creating his own narratival conception “frei nach” astrology-mythology-astronomy.²

Holst was reading Alan Leo’s What is a Horoscope and How is it Cast? while he was composing The Planets, and he was enthusiastic in his exploration of astrology.³ Holst’s daughter Imogen, however, asserts that “horoscopes had nothing to do with the writing of The Planets, and once he had taken the underlying idea from astrology, he let the music have its way with him” (I. Holst 1958, 44).⁴ Significantly, Holst did not include the Sun and the Moon—which are considered “planets” in astrology—but he did include Uranus and Neptune, which are not acknowledged by the classical astrology of Holst’s time. And even though Mercury is the third movement of the finished work, it was originally listed as “no. 1” in his sketch notebook—an indication that Holst was thinking of its position as the first planet from the Sun.

As for the widespread assumption that The Planets are character portraits of the ancient gods of Greco-Roman mythology, Holst “was a bit annoyed when certain newspapers dragged in bits about Zeus in The Planets,” averring that “the legends about Greek and Roman gods have nothing to do with it” (I. Holst 1981, 55). While he did assert that his movements were “not [suggested] by classical mythology,” Holst may not have been aware of the extent to which mythology, astrology, and astronomy were intertwined in popular conceptions of the planets.⁵  For example, Holst likely labeled his Mars as “The Bringer of War” because the astrological symbol is a shield and spear, and the horoscope is characterized by aggressiveness and strength. Astrology borrowed this war-tinged image of Mars from Roman mythology, which designated Mars as the god of war. And the Romans arrived at this martial conception from astronomical observation that revealed the planet’s radiant red color, which human imagination equated with fire and heat and blood(shed). The same type of lineage can be traced for Venus (astronomy’s luminous, soft-hued orb → mythology’s goddess of love → astrology’s emotion, love, and beauty → Holst’s “Bringer of Peace”) and the other planets as well.

Although astronomy figured strongly in Holst’s planetary depictions, he was not bound by astronomical considerations. He did not include the planet Earth, and he deviated slightly from the solar system’s planetary ordering by swapping the positions of Mercury and Mars. Holst made the intriguing choice to make Mars the first planet in his solar system, and it was the first movement of the suite he composed. This reordering of the planets is an important first clue for understanding the nature of the journey Holst envisioned, as agitated strife is the port from which his voyage departs.

2. The Journey

2.1 Impetus

“I have a longing to be by myself” was Holst’s mantra throughout his life (I. Holst 1958, 90). According to Clifford Bax, Holst was “feeling rather tired of life” during the period before he began composing The Planets (Short 1990, 126). The noise and crowds and bustle of daily life in London, the pressures of his all-consuming teaching duties, and his exhausting schedule were all taking a toll on his spirits. According to Imogen, “He hated having to waste time on social engagements instead of getting on with his own work” (I. Holst 1981, 54), and he felt that the various demands on his time and energy corroded his peace of mind.⁶ It was from this perturbed, agitated mood that Holst began composing Mars. Soon after its founding, the St. Paul’s Girls School built a special soundproof room for Holst, and this room immediately became a sanctuary of profound importance for the weary composer. He began retreating into this oasis of isolation to escape the world around him, and he spent ever more time locked away in that room. Imogen recalls that “he used to look forward to what he called the ‘spell’ of his room, where he could shut himself up at the end of a busy week and forget everything except what he was composing” (I. Holst 1981, 49). The remaining (non-Mars) movements of The Planets were written in this soothing and spacious sanctum, as well as weekend and holiday work in his tranquil Thaxted cottage retreat, to be discussed later.

2.2 Love of Travel

“The time I was writing The Planets . . . was the happiest period of composition that I’ve had” (Bax 1936, 60). Holst’s statement might speak to the delight one feels while planning a much-needed holiday; the most important release is in the psychological escape of anticipation, even if the journey never physically comes to fruition, as sociological researchers have shown (Nawijn et al. 2010; Van Boven and Ashworth 2007). Holst loved to travel and explore new places, but his busy schedule prevented him from traveling as much as he would have liked. He was not fond of the modes of travel, however, finding them noisy and crowded and exhausting, as attested by this quote from later in his life:

If I ever cross the Atlantic again I want a most exclusive cabin in a very fast boat . . . to keep undesirable people away. But what I really want is to keep off the sea altogether. I’m fed up with the ship . . . and the passengers . . . and above all the noise. (I. Holst 1958, 137)

Holst longed for a smoother, quieter, more solitary mode of travel. Although impractical for long-range travel, walking was Holst’s favorite way to relax and spend his holidays. Imogen recounts that “most of his walks were solitary, to enable him to go on thinking of the music that was in his mind” (I. Holst 1981, 78). He actually found his beloved home in Thaxted during a five-day walking expedition, and his family recalls that he was enthralled by the magnificent silence and solitude of the countryside cottage. It seems natural, then, that Holst would plan his grandest expedition ever in search of silence and solitude.

2.3 The Musical Journey

An excursion into the celestial sphere was a natural choice for Holst, being the most reclusive travel destination imaginable. Before selecting the solar system as the destination for his journey, India was Holst’s first foray into musical travel. Although Holst never had the opportunity to visit India, he immersed himself in the study of Sanskrit texts and Hindu legends and hymns while composing his Indian-inspired opera Sāvitri (1908),⁷ much in the same way he would later become engrossed in the study of astrology and astronomy while composing The Planets. Like his imaginary India, Holst constructed his solar system (“his chosen other world” [I. Holst 1981, 25]) through a combination of research and reverie. Holst referred to The Planets as “a series of mood pictures” (Short 1990, 121), a quote that ostensibly refers to the mood of each planet as a mythological or astrological character. However, in the context of the esoteric narrative, we propose that the moods Holst was capturing were his own.⁸ The following section traces a trajectory of these personal moods from oppressive stress to blissful calm.

2.4 Ports of Call

2.4.1 Mars

The most popular misconception about this most popular movement is that it was intended as a representation of warfare ignited by the eruption of World War I. However, Holst emphatically and repeatedly proclaimed that Mars had nothing to do with war, and that he had in fact completed it before the war even began (Greene 1995, 19).⁹ As mentioned earlier, Mars was the only movement not written in the tranquility of his soundproof room, a space built to insulate its occupant from the turbulence expressed musically in this movement. This movement is a maelstrom of dissonance, tension, crowded commotion, blaring din—all the things that were perturbing him at the time (and were likely among the factors that eventually led to one of several nervous breakdowns). The “hypnotic repetition” of the $$^{5}_{4}$$ rhythm in this movement was apparently inspired by a holiday in Algeria, where Holst was mesmerized by the rhythms he heard (Short 1990, 87). This is the only movement in which rhythm dominates over other musical elements, and Bernard Shore makes the interesting (if antiquated) claim that, unlike the individualistic nature of melody, “rhythm is communal and a tyrant to the individual” (Shore 1949, 321). Rhythm does bear an overbearing role in Mars, and Holst brandished it effectively to represent the relentless bustle and battle of society.¹⁰ He chose Mars as the point of departure for this journey in order to depict what he was escaping.

The conclusion of Mars, clearly articulating a tonic of C, features a jarring vertical collision of the tonic and Neapolitan chords (roots and fifths only: {C, G, D$$\flat$$, A$$\flat$$}), an effect which Holst first employed (with the same pitch-class roots of C versus D$$\flat$$) at the end of his setting of Psalm 86, To My Humble Supplication (1912), accompanying the following text (Short 1990, 99):

That my steps Thy paths may tread
Which to endless bliss do lead.

In this psalm setting, the tonic-Neapolitan clash occurs directly on the last verse, and this intertextuality imports a hint as to where his interplanetary journey will lead (“endless bliss”).

The Mars movement also encapsulates the turbulent initial passage of the voyage. As Holst experienced in his sea travels, ships must navigate through the treacherous turbulence of choppy tides before entering the calm passage of smooth waters. Venus is that calm passage.

2.4.2 Venus

Venus is the tranquil sea attained after a rough crossing, and the pulsating alternation of harmonies emblematic to Venus is borrowed from the end of the last movement of Vaughan Williams’s Sea Symphony (1909).¹¹ There is an inherent sense of metric, harmonic, and dynamic liberation in Holst’s Venus movement, after escaping the assault of Mars. It may not be the final destination, but it provides the traveler a bit of relief (solitude) from the constraints left behind (society).¹² Venus features a number of solo melodies, celebrating the solitude of the individual after the communal clamor of Mars, and the opening horn solo almost evokes the sigh of relief Holst must have breathed upon entering the sanctuary of his soundproof room. This planetary sojourn features soothing pastel shades of sound (as opposed to the glare of Mars’s piercingly vivid chroma), comfortable meters (after the discomposing irregularity of Mars’s $$^{5}_{4}$$ meter), and gently swaying rhythms. And, with the exception of the horns, the brass section, which dominated Mars, remains silent during this movement to allow the weary traveler a chance to convalesce in a less blaring environment.

2.4.3 Mercury

Mercury was the last movement Holst composed, and it is the least purposeful of all the movements—“a mere activity whose character is not defined” (Greene 1995, 52). This movement is a constant chase without any particular object of pursuit—B$$\flat$$ Major chases A Major, $$^{6}_{8}$$ chases $$^{3}_{4}$$ —reminiscent of the purely somatic play of animals (for example, frolicking puppies chasing their tails and wrestling aimlessly). At Mercury the rejuvenated traveler is now ready for diversion, for “escape to a sphere of divine playfulness” (Shore 1949, 318).

2.4.4 Jupiter

Jupiter is the only movement with an overtly gregarious and jovial temperament. At this point in the journey the traveler has been sufficiently refreshed, to the point of reminiscing fondly about good times spent with dear friends. Significantly, this movement that celebrates customary social interaction is also the only movement that recollects conventional sonata form and conventional tonality. The grandiosity of Jupiter is analogous to the enormity of its namesake planet (the largest in our solar system), as well as the dominion of its namesake Roman god (king of the gods). Because of its musical assertiveness, Jupiter has commonly been treated as the pinnacle of The Planets. Early performances of the work often ended with the Jupiter movement, and the prevalent early discussions of a “double symphony” scheme were entirely based on lionizing Jupiter as the apotheosis of the suite.¹³ Holst hated this; as Imogen recounts, “he particularly disliked having to finish with Jupiter to make ‘a happy ending’” (I. Holst 1981, 51). Despite the public’s attraction to the jubilant spirit, thematic majesty, and formal robustness of the Jupiter movement, Holst viewed it as an intermediate, temporary stopping point on his journey.

2.4.5 Saturn

This movement is where the quest for solitude enters the next phase, as from the world of society and human life the traveler now prepares to depart. Holst did not fear old age, but embraced it with pleasure: the “Bringer of Old Age” was his favorite movement of The Planets, though this was decidedly not the prevalent preference (“people seem to dislike Saturn which is my favourite” [I. Holst 1958, 76]). Music scholar Reginald Morris, in a 1920 article for the Athenaeum, described the amusing scene of elderly patrons tottering uneasily out of the concert hall during the Saturn movement, shaken by Holst’s powerful portrayal of old age: “Quite a number of old ladies in our neighborhood were seen to rise from their seat, stagger for an instant, and then feel their way, feebly but with evident determination, towards the exit” (Short 1990, 130). Holst utilized a hollow, ghostly ostinato of two alternating ninth chords “to suggest the inevitable passage of time and the process of ageing” (Short 1990, 129). According to his student Dorothy Callard, Holst was inspired to depict old age with two alternating chords after visiting Durham Cathedral, where two bells were tolled by “two very old men in black gowns, very slow and solemn” (Short 1990, 129). Holst’s positive view of aging also aligned with Leo’s horoscope, which characterized Saturn as “thorough and enduring,” having “a firm hold on life,” and possessing the “virtues of industry, economy, thrift, patience, prudence and chastity” (Leo [1913] 2003, 60). The Saturn movement traces the evolution of the traveler’s aging process, from its gradual creeping onset, mounting to a brief crisis of denial and struggle (rehearsals II to V), resolving to an epiphany of resignation and acceptance (rehearsal V), and then finally moving on (m. 117 to the end).¹⁴ The beautiful resignation that occurs at the Andante (rehearsal V) is especially striking because of the stunning contrast it bears to the rest of the movement. All instruments drop out except the harps and strings, leaving a pure, celestial sound that is perhaps Holst’s vision of the beauty of eternity to come, a vision that will be crucial in the Uranus movement. This epiphany provides the comfort and strength needed to accept old age with grace and even gladness. Holst looked forward to proceeding to the next phase of life. (Regarding a near-death experience in 1932, Holst recalled: “I had one beautiful experience. I felt I was sinking so low that I couldn’t go much further and remain on earth. And, as I have always expected, it was a lovely feeling” [I. Holst 1981, 81].) Describing his Saturn movement in a letter to conductor Sir Adrian Boult, Holst said it “must begin from another world and gradually overwhelm this one” (quoted in Short 1990, 130). Or, as Ghuman (2014, 147) puts it, “The music, and Saturn itself, relents, freeing the traveller to be guided into the afterlife. Death is welcomed in archaic counterpoint.”

2.4.6 Uranus

The full title of this movement is Uranus, the Magician. The obvious similarities between Holst’s Uranus and Dukas’s Sorcerer’s Apprentice (1897) have been cited by many. There are also resemblances in Uranus to the appearance of the wizard in Holst’s The Perfect Fool (1922), as well as parallels to the wizard in his Phantastes Suite (1911). What do all these references to magic and the occult signify in the context of Holst’s planetary voyage? Judging by the grotesque playfulness and parody in the music, as well as the horoscope description of “eccentric, strange, and erratic” (Leo [1913] 2003, 61), this movement might be said to depict some sort of pre-death delirium or hallucination. Irrational images are flitting across the feverish intellect, and a terrifying, relentless motive (<G, E$$\flat$$, A, B>) plagues the weakened mind.¹⁵ The dissonant, thunderous ffff shriek one measure before rehearsal VIII is the final death throe instigated by the purely corporeal survival instinct, which clings fiercely and desperately to life when the end is near (despite any higher levels of brain function that may take comfort in the idea of a beautiful afterlife).¹⁶ What follows is the suspension of time and matter, as the strings alone sustain a hushed pp whole-tone chord. In allusion to the celestial “resignation” in the previous Saturn movement, the texture drops down to just strings and harps.¹⁷ The first harp plucks the main motive in eerie harmonics, which conjures the impression of a ticking clock as the angel of death awaits the ascending soul. Ten measures later at rehearsal IX (m. 231), the winds and timpani take over in the form of three dwindling outbursts (fff – mf – pp) as the fading body lashes back in its final attempts at life. After the last of these vain attempts, the texture is reduced once again to ppp sustained strings and the plucking harmonics of the harp, and the traveler’s eyes have closed for the very last time.

2.4.7 Neptune

Neptune, the traveler’s final destination, is a strange and beautiful place. The planet Neptune is so remote that its stately circumambulation around the Sun takes 165 (Earth) years, which Holst’s Neptune simulates with its calm, unhurried procession. The chilly character of the music conveys Neptune’s frosty –214ºC temperature with shimmering string tremolos that imply the reflection of distant sunlight on ice, and quivering harps and celesta that suggest exquisite glimmering icicles. This is not the kind of heaven Fauré (in his Requiem) or Haydn (in his Creation) envisioned. Holst’s heaven in The Planets is gorgeously desolate and enigmatic, rather than bustling with warmth and love. Neptune operates under a consistently hushed pp without any (notated) dynamic swells, and we must strain to hear the sound emanating from this mysterious planet at the remotest edge of our solar system. As the planet slowly rotates we perceive the beguiling mystical music of sirens, calling weary travelers to the promise of eternal peace.¹⁸ With its harps and wordless female choir, Neptune evokes heaven with its host of angels. Holst’s decision to include a choir in Neptune is an intriguing indicator of the metaphysical narrative encapsulated in The Planets. Holst also used “the remote sound of a wordless female chorus” in his India-inspired, death-themed opera Sāvitri, with the chorus singing to represent “the divine world interacting with the mortal,” and then again “when Death reappears” (Matthews 2000, 3).¹⁹ As in Neptune, Holst specified “a hidden chorus of female voices” for creating this mystical effect (Holst [1916] 1973, 1). Speaking of the 1916 Thaxted music festival, Holst revealed his special connection to choral singing:

I realize now why the bible insists on heaven being a place (I should call it a condition) where people sing and go on singing. We kept it up at Thaxted about fourteen hours a day. The reason why we didn’t do it more is that we were not capable mentally or physically of realizing heaven any further. . . . Music being identical with heaven, isn’t a thing of momentary thrills, or even hourly ones. It’s a condition of eternity. (I. Holst 1981, 43)

Thus, Holst employed the choir in Neptune to end his voyage because it represented the ideal vision of his final heavenly home.²⁰ Holst first used his echo choir effect, which involves two separate and identical choirs, in his setting of “The Splendour Falls” (1905) from Tennyson’s The Princess (Short 1990, 62). Here is the Tennyson text that accompanies the echo choir effect, with the lines especially relevant to Neptune underlined:

O love, they die in yon rich sky,
They faint on hill or field or river;
Our echoes roll from soul to soul,
And grow for ever and for ever.
Blow, bugle, blow, set the wild echoes flying,
And answer, echoes, answer, dying, dying, dying.

This intertextual relationship imbues meaning to the Neptune ending, in which the traveler drifts slowly out into the vast eternity of space, never to return again.

The entire movement is pp, fading to pppp at the end, and finally fading away into utter nothingness. The fadeout was a completely innovative way to end a work, and Holst was demanding about ensuring that the effect be executed perfectly.²¹ On this journey the fadeout functions on two different levels: physically the traveler is drifting beyond the gravitational pull of our solar system into the infinite vastness (and silence) of outer space, and spiritually they are ascending above the material world into the infinite realm of heaven.

3. Pitch-Class-Set Proxemics

3.1 A New Measure

Each movement of The Planets features strikingly memorable motivic and chordal ideas, the most distinctive of which figure prominently at the beginning and ending of each movement. The succession of these ideas over the course of the work, when analyzed from a particular perspective, may be shown to fit the narrative we have just presented—progressing from a state of crowdedness to sparseness. Although The Planets arguably conforms to idioms more tonal than non-tonal, our approach (consistent with precedent post-tonal analyses of tonal music) considers these motives as pitch-class sets distinct from an affiliation with a tonic or other common-practice conventions.²²

While analogizing social crowdedness with pitch-class proximity (the inverse of what music theorists call “maximal evenness” [Clough and Douthett 1991]) seems an obvious choice, there are at least three ways in which this approach falls short for our purposes. First, a harmony with more pitch classes, like a chord composed of all six members of a whole-tone scale (6–30[02468T]), may be just as maximally even as a harmony with fewer pitch classes, like an augmented triad (3–12[048]), but the former will likely contain more pitch-class crowding and dissonant impingements. Second, even if one controls for the size of the set, Holst’s harmonic language does not fully avail the extremes of proximity and the extent of their psychological difference that would be appropriate to model the difference between the busy streets of London or an accosting member of the press, and the tranquility of Thaxted or his soundproof office at St. Paul’s Girls School. The musical analogs of these extremes for some sizes of set—such as the four-note minimally even 4–1[0123] and the maximally even fully-diminished seventh 4–28[0369]—would be out of stylistic character as thematic harmonies in Holst’s music in general and in The Planets in particular. Third, this analogy between maximal evenness of the pitch classes of a chord and the maximal sparseness of a populace decentralizes and depersonalizes the members of the populace. This makes such an analogy more fitting for a group’s collective anxiety about proximity and less fitting for that of a single individual (like Holst). Ideally, the musical elements analogous to Holst and another person who encroaches upon Holst’s personal space would have more of a particular character than two undifferentiated pitch classes within a pitch-class set.

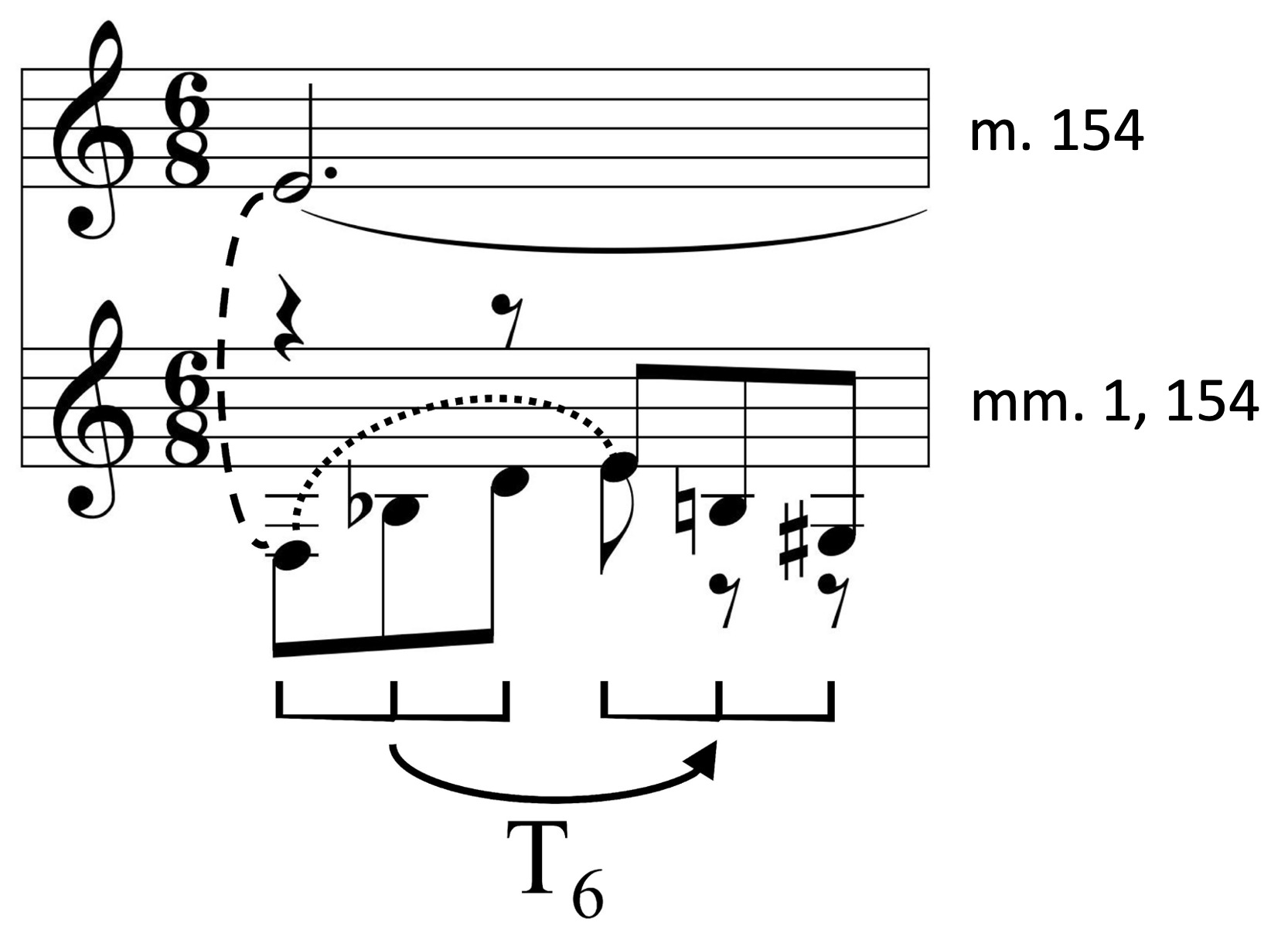
One solution to this third shortcoming is to measure not the relative mutual proximity of multiple undifferentiated pitch classes within a pitch-class set, but rather the mutual proximity of two distinctive sets. A hallmark of many of the beginnings and endings of the movements in The Planets is the juxtaposition or overlap of a three-note motive or harmony with another in the same set class. Example 1 demonstrates this by analyzing the beginning of the first six movements and the ending of the last movement. (Labels in captions will be defined in due course.) For instance, one can interpret the expansion of the initial three-note motive for Mars (<G, D, D$$\flat$$>) to the cyclical four-note idea (<G, D, D$$\flat$$, A$$\flat$$>) through imbrication: just as the first, second, and third notes belong to the 3–5[016] set class, so do the second, third, and fourth notes, sharing the <D, D$$\flat$$> semitone. These analyses further relate Mars’s beginning to Uranus’s primary four-note motive, shown in Example 1f: although it is generated by 3–8[026] instead of 3–5[016], two members of this set class overlap in the same fashion as Mars’s opening four-note idea.

Example 1. Measures of closeness for two three-note sets (marked in square brackets) in the same set class during some beginnings and endings in Holst’s Planets. Harmonic and melodic presentations of SID intervals are shown with dashed and dotted lines, respectively.

Other beginnings and endings also conform to this configuration of what may be called a “transformational combination” of trichords, even though they may use different set classes and textures.²³ The opening of Saturn (Example 1e) anticipates the combination of two overlapping 3-8[026]s of Uranus’s four-note idea, but with transpositionally-related three-note harmonies instead of inversionally-related successions of three notes. Jupiter (Example 1d) generates its opening pentatonic blur using the transpositional combination of two quick 3–7[025] motives. The other transformational combinations in Example 1 involve the consonant triads of set class 3–11[037]. The excerpt from Example 1 that breaks down into 3–11[037]s most clearly is the opening of Mercury (Example 1c), with its alternation of tritone-related arpeggiated major triads. The very opening of Venus (Example 1b) uses a major seventh chord, and the fadeout ending of Neptune (Example 1g) alternates a dominant ninth chord with the aforementioned minor seventh chord. All three types of extended tertian chords may be disassembled into two overlapping 3–11[037]s, unlike many other extended tertian chords, such as the dominant seventh, half-diminished seventh, and fully-diminished seventh. To be sure, the major seventh chord and minor seventh chord could also be disassembled into other overlapping trichords of the same set class: 3–4[015] and 3–7[025], respectively. However, in these chords’ voice-leading contexts (parallel motion within, and contrary motion between), two voice-leading streams best supports their disassembly into 3–11[037]s.

Each of the instances in Example 1 thus brings mutually close in temporal space two members of the same set class; this pair can symbolize two people—such as Holst (as our “author”) and another person such as a student, devotee, publisher, impresario, or even a passing stranger. However, these pairs of sets vary in how mutually close they are in pitch space. The measurement of smallest individual displacement, or SID, is one way to calculate the degree of this mutual pitch proximity. For two pitch-class sets X and Y, such that 1) X and Y are not multi-sets (i.e. contain no duplications of the same pitch class) and 2) X is not equal to or a subset of Y, and vice versa, SID is the smallest unordered pitch-class interval between—that is, the smallest interval class for—a pitch class in X that is not in Y and a pitch class in Y that is not in X. In other words, the SID of two pitch-class sets measures the smallest possible semitonal distance between the parts of the two sets that are distinct from the sets’ overlap. This calculation deliberately ignores intervals within the intersection of X and Y because they fail to distinguish between the two sets as analogous to distinct individuals; this shared space is the antithesis of private, personal space.

For example, the opening of Mars overlaps the 3–5[016] sets <G, D, D$$\flat$$> and <D, D$$\flat$$, A$$\flat$$>. There is only one pitch class in each set that is not in the other: G for <D, D$$\flat$$, A$$\flat$$> and A$$\flat$$ for <G, D, D$$\flat$$>. Since G and A$$\flat$$ span an unordered pitch-class interval of 1, the SID of <G, D, D$$\flat$$> and <D, D$$\flat$$, A$$\flat$$> is 1. As another example, the F⁹ chord in the fadeout of Neptune breaks down into the 3–11[037] sets {F, A, C} and {C, E$$\flat$$, G}. F and A are in {F, A, C} but not in {C, E$$\flat$$, G}, and E$$\flat$$ and G are in {C, E$$\flat$$, G} but not in {F, A, C}. Since the smallest unordered pitch-class interval from either F or A to either E$$\flat$$ and G is 2 (F and E$$\flat$$, or F and G, or G and A), the SID of {F, A, C} and {C, E$$\flat$$, G} is 2. Since SID always yields an interval class, its smallest possible value is 1 and its largest possible value is 6 (for the usual chromatic size of 12). However, for two sets of size m and n, their SID measurement cannot exceed $$7-\lceil\frac{\left(3+3\right)}{2}\rceil\text{, }\hspace{12pt}$$ where $$\lceil\rceil$$ is the ceiling function, which rounds up to the next integer. For an example that corresponds with the size of the sets in the two aforementioned examples, the SID value between two trichords $$\left(m = n = 3\right)\hspace{12pt}$$ must range between 1 and 4 $$\left(7-\lceil\frac{\left(3+3\right)}{2}\rceil\right)\text{.}$$

Compared to other measurements, SID, especially when reckoned between trichords, well analogizes the measure of a proxemic relation. Anthropologist Edward T. Hall laid much of the groundwork for the field of proxemics, which includes the study of the amount of space people wish to have between themselves and others.²⁴ In his 1966 book The Hidden Dimension, Hall divides the continuum of human interpersonal distance into four discrete categories: intimate space, personal space, social space, and public space (Hall 1966, 108ff). Hall’s quadripartition conveniently matches the number of possible SID values between trichords, the size of set chosen for the present analysis. Furthermore, a consistent theme in Hall’s proxemic analyses is that conditions and behaviors associated with a space activate primarily when this space is breached rather than saturated. The Mars analysis from the previous paragraph measured a SID value of 1 between the trichords <G, D, D$$\flat$$> and <D, D$$\flat$$, A$$\flat$$>. The same SID value of 1 spans the trichords <G, D, D$$\flat$$> and a hypothetical stand-in of <A$$\flat$$, E$$\flat$$, C>, even though three separate semitones—G and A$$\flat$$, D and E$$\flat$$, and D$$\flat$$ and C—instead of one semitone extend between the trichords. Although the hypothetical pair of trichords could express more biting dissonance, especially if realized as a six-note verticality, than Mars’s pair, what matters to the SID measurement is that the “ic1 zone” has been intruded upon, even if minimally so, analogous to how even a slight touch of two bodies can trigger an experience of intimacy or recoil. (Nonetheless, later in this essay we will find the number of semitones that span the pair of sets analytically useful as a secondary and subcategorical measurement, related to how Hall subdivides each of his four spaces into a “close phase” and a “far phase.”)

Example 1 provides the SID value for the pair of transformationally related trichords in each excerpt. (The other values will be described later.) For each excerpt of Example 1, two notes—one in each trichord—that span the SID interval are connected with a dashed line if the notes overlap in time—that is, produce a harmony—and with a dotted line if they do not occur simultaneously at some point. This analysis advances the analogy that the degree of unease associated with interpersonal nearness corresponds with the degree of harmonic dissonance in particular. Of course, any transformational combination of the two trichords that produces a single chord, like the beginning of Venus or the end of Neptune, comports with this analogy. However, of the other more melodic trichordal combinations, Holst’s deployment of them still makes at least one of the SID intervals a harmony, shown in Example 1 with at least one dashed line for every excerpt. This SID harmony either occurs right away, as in the beginnings of Mars, Jupiter, and Uranus, or during a recapitulation of the opening material, as in Mercury and Saturn. (Example 1 shows the two instances of the latter by putting the beginning and the recapitulation in the same system.)

From this perspective, the beginnings and endings excerpted in Example 1 neatly organize: the excerpts from the first three movements (Mars, Venus, and Mercury) project a SID of 1, and the excerpts from the last four movements (Jupiter, Saturn, Uranus, and Neptune) project a SID of 2 or greater. Remarkably, the SID scores of 2 or higher hold across a variety of macroharmonies, from Jupiter’s introductory pentatonicism, through the whole-tone subsets that open Saturn and Uranus, to the enneatonic (9–12[01245689T]) fade out of Neptune; all six semitones among the nine pitch classes in this fadeout avoid harmonic simultaneity in the offstage female chorus’s final two extended-tertian chords. Admittedly, this musical analog to a fantastical metaphysical voyage from crowdedness to spaciousness is coarsely gradated. However, all seven movements participate in the terraced change from a half-step proximity to at least a whole-step proximity. Moreover, the categorization by SID score into two distinct groups—the first three movements with a tighter SID of 1, and the last four movements with a looser SID of 2 or greater—perfectly matches the solar system’s terraced progression from the densely packed terrestrial planets of Mercury, Venus, and Mars to the widely spaced gas giants of Jupiter, Saturn, Uranus, and Neptune, as illustrated in Example 2. (And in addition to their tight spatial arrangement, terrestrial planets are themselves considerably denser than the rarefied gaseous planets, being composed of rock rather than gas.)

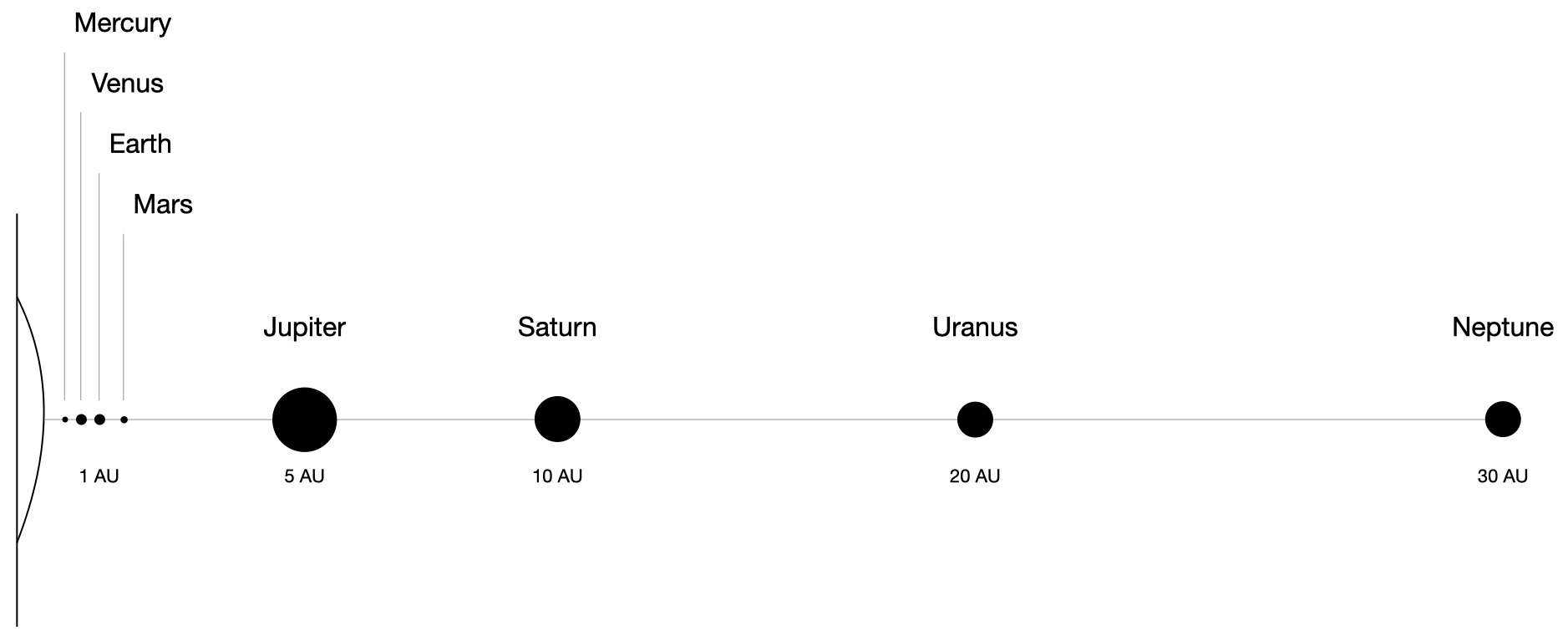
3.2 Adjusting for Context

The field of proxemics recognizes the psychological difference that context can play in one’s assessments of the anxiety that the close presence of another creates. In his 1975 book The Environment and Social Behavior: Privacy, Personal Space, Territory, Crowding, Irwin Altman makes a distinction between density (the number of people per unit of area) and crowding (the discomfort caused by the violation of personal space). Individual aversions aside, one tends to be more accommodating of crowding when the density of the environment is relatively high, as in a crowded elevator or subway car. When an instance of two people brushing past one another on a bustling city sidewalk is transported to an otherwise deserted country lane, substantially lowering the density, the experience of crowding considerably increases despite the invariance of “yardstick distance” between the two persons.²⁵ This qualifying context for interpersonal proximity plays an important role in Holst’s biography: his soundproof room at St. Paul’s Girls School is valued not only because of its spatial and sonic cushion, but also because this cushion is located with the congested and loud surroundings of a lively and urban academic environment. Such a room would be much less necessary and valued in the sparsely populated cottage town of Thaxted.

The analysis of Holst’s music using SID easily adopts an analog of this form of contextual proximity, which in turn further strengthens the connection between the musical and personal treks through Holst’s solar system. While not a requirement of calculating SID, all of the excerpts in Example 1 measure the SID score between two sets of the same set class. Some sets are more likely to achieve a higher or lower SID score when compared to another randomly chosen set from the same set class, depending upon which set class is used. For example, <G, D, D$$\flat$$>—the opening three-note motive from Mars—is in set class 3–5[016]. Of the twenty-three other members in 3–5[016], <G, D, D$$\flat$$> achieves a SID score of 1 with thirteen of them (including the aforementioned <D, D$$\flat$$ A$$\flat$$>), a SID score of 2 with seven others, and SID scores of 4, 5, and 6 with the remaining three. This means that the 3–5[016] set class has an average smallest individual displacement, or AVGSID, of around 1.83 $$\left(\frac{1\times13+2\times7+4+5+6}{23}\right)\text{.}\hspace{12pt}\hspace{12pt}\hspace{12pt}$$ The higher the number, the less dense the set class, not in terms of the maximal evenness of the pitch classes in any member of the class, but rather in terms of average mutual leeway between any two members of the class. Table 1, which provides the AVGSID values for all twelve trichordal set classes, makes clear this difference: relatively even trichords like 3–12[048] and 3–11[037] have a relatively low AVGSID—that is, they tend to rub up close. Conversely, relatively lumpy trichords like 3–1[012] and 3–2[013] have a relatively high AVGSID—that is, they tend to offer more room to maneuver.

Set class	AVGSID
(037)	1.09
(048)	1.33
(025)	1.48
(027)	1.55
(036)	1.82
(015)	1.83
(016)	1.83
(026)	1.83
(013)	2.00
(014)	2.04
(012)	2.36
(024)	2.55

This extra room afforded to sets like 3–1[012] and 3–2[013] as measured by AVGSID can be most readily noticed by observing how sequestered all of the members of sets like these are on a relatively small patch of the circle of twelve pitch classes organized by semitonal adjacency. Pick any two 3–1[012]s at random, and the closest distance on this circle between their non-overlapping parts is likely to be greater than the same for any two 3–11[037]s chosen at random. This is because any 3–11[037] has spread itself out over much of the pitch-class circle, like an intrusive empire with colonies across the globe, and a 3–11[037] empire is quite likely to have one of its borders near that of another 3–11[037] empire.²⁶ However, the values in Table 1 do not quite correlate to these sets’ degrees of evenness; for example, 3–12[048] and 3–1[012] are the most and least even sets of the twelve trichordal set classes, but 3–11[037] and 3–6[024] have the lowest and highest AVGSID values. This discrepancy derives from the boost that a set class receives by being a subset of a symmetrical scale like the whole-tone scale, which contributes to more instances of more shared pitches among all possible pairs of sets in the class. This reduces the number of places in which a “private,” unshared pitch class in one set can encroach upon the same in another.

The context of AVGSID, which is analogous to this contextual density of persons, particularly in terms of “personal” proximity, avails an adjusted SID, or ADJSID, that accounts for this context: ADJSID = SID/AVGSID.²⁷ When ADJSID is 1, the experience of proximity is what one expects given a context. An ADJSID that is lower than 1 represents a closeness that is more than what one should have in a certain context, akin to one rubbing elbows with another even though no congestion justifies this contact. An ADJSID that is higher than 1 represents a sparseness that is more than what one would normally have in a certain context, akin to extra “elbow room” in otherwise tight quarters. Musically speaking, an ADJSID lesser or greater than 1 means (in most scenarios) that any abrasion of secundal dissonance between two chords is probably more or less, respectively, than one would face if two chords from the same set class were chosen at random.

Example 1 provides the AVGSID and ADJSID values for all of its excerpts, and Example 3 additionally places these ADJSID values on a graph that shows how these values change as the suite unfolds in time. (The thin arrows will be explained in the following subsection.) As shown in Example 3, ADJSID subdivides SID’s two aforementioned rising terraces (partitioned with a thick line) into four groups of continuously rising values (partitioned with lines thick and thin). Mars opens with a transformational combination of two 3–5[016]s, instead of two 3–11[037]s whose transformational combination opens Venus and Mercury. Since 3–5[016] has a higher AVGSID than 3–11[037], there is a higher likelihood that the harmonic combination of two 3–5[016]s will produce a less harsh whole step than the more harsh half step. Nonetheless, Mars’s second 3–5[016] sounds this more harsh half step, and thus the ADJSID of Mars’s beginning is consequently the lowest of all of the movements. In the proxemic analogy, this nadir parallels those unfortunate episodes that Holst despises when some member of society actively, rather than passively, impinges upon him (such as someone who approaches him with the request for an autograph).

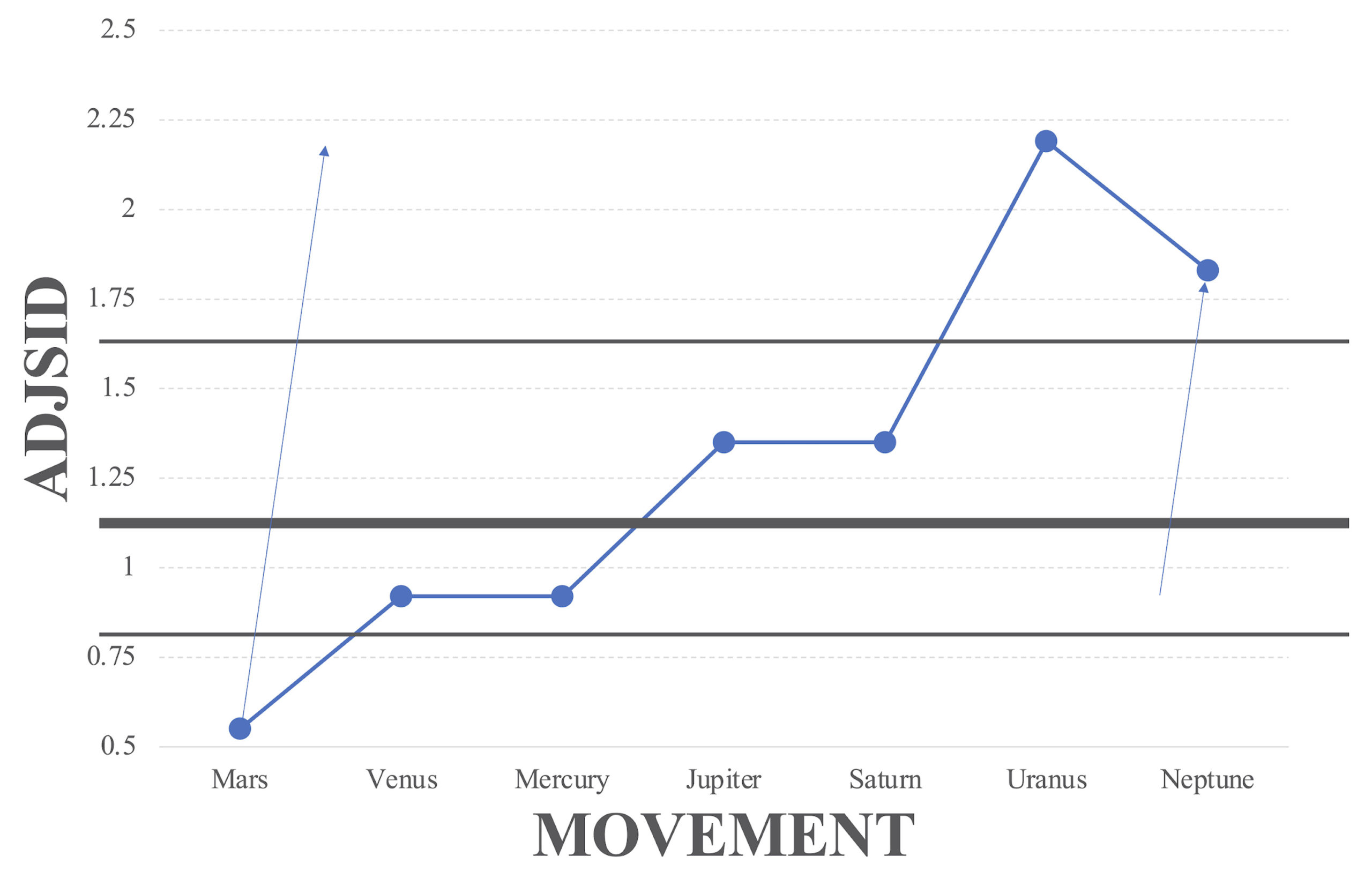
By contrast, the progression to Venus’s and Mercury’s 3–11[037] openings eases the tension a bit, not by taking away the semitonal harmony that results from the transformational combination, but by shifting the set-class environment to a context that is considerably more likely to produce such a semitonal overlap. Example 4 shows this higher likelihood with more detail. The twenty-three chord pairs in Example 4 represent all of the ways two different members of 3–11[037] can be placed in succession, up to transpositional and inversional equivalence. The top system relates two triads by the eleven non-identity pitch-class transpositions, and the bottom two systems relate triads by inversion around C and C/C$$\sharp$$, respectively. These twenty-three pairs correspond to the twenty-three Riemannian ordered relations between different consonant triads, up to equal-tempered equivalence. Every semitonal pair spanning two triads of a pair is indicated with two notes of the same non-black color of notehead. If a pair of triads has at least one such pair of non-black noteheads, that pair has a SID of 1. Only two triad pairs—the first two pairs on the second system—use exclusively black noteheads; they have a SID of 2. The decrease in AVGSID, and hence increase in ADJSID, as the suite moves into Venus and Mercury, parallels how one can more willingly (if also begrudgingly) concede private space or attention if one is surrounded by more people, knowing that the odds of receiving such demands are inherently higher in such social conditions.

The change to higher ADJSID values for the next three planets reflects the change to higher SID values of 2 (Jupiter and Saturn) and 4 (Uranus). However, the higher AVGSID values for these movements anticipate correspondingly higher ADJSID values. This scenario might symbolize a visit to the country: one is grateful for a wider interpersonal clearance and a quieter soundscape, but this is what one expects when in the country. In fact, as high as these SID values are, they could be even higher: 3–7[025] can enjoy SID values as high as 5 (e.g., {C, G} for {C, D, F} and {D, F, G}), and 3–8[026] can enjoy SID values as high as 6 (e.g., {D, G$$\sharp$$} for {C, D, F$$\sharp$$} and {F$$\sharp$$, G$$\sharp$$, C}). An arguably even more impressive accomplishment in psychological solitude would be to bring this physical and sonic capaciousness into a setting that typically lacks it, and to maximize its achievement. In Holst’s life, this was accomplished by his large, soundproof room at St. Paul’s Girls School. In Holst’s work—using the analogy facilitated by ADJSID—this is accomplished by the last two chords of the piece: Neptune’s fadeout. As discussed earlier, this fadeout oscillates between a dominant ninth chord (F⁹: {F, A, C, E$$\flat$$, G}) and a minor seventh chord (C$$\sharp$$m7: {C$$\sharp$$, E, G$$\sharp$$, B}). These two extended tertian chords can be interpreted as transformational—specifically, inversional—combinations of 3–11[037] triads. On the one hand, this is a return to the 3–11[037] combinations from Venus and Mercury, and, given 3–11[037]’s low AVGSID—maximally low for a trichord—a return to the teeming urban mass. On the other hand, these two triad pairs are exactly the only two triad pairs of the twenty-three in Example 4—again, the first two pairs on the second system—that have the 3–11[037]’s maximally high SID of 2. Therefore, although the graph of Example 3 has a slight downturn from Uranus to Neptune, the latter is nonetheless very special in other respects. Neptune’s conclusion exclusively presents not just the only two combinations of consonant triads that avoid strident semitonal harmony, but also the only two combinations of trichords with the lowest AVGSID that maximize the SID for that set class. Holst finds within the most clamorous universe of trichordal overlaps a tiny niche of maximal harmonic tranquility, which, in the fadeout, gradually usher the listener toward blissful quietude.

3.3 Contracted Versions of the Journey

Mirroring on a smaller scale the entire suite’s journey, both the first and last movements of Holst’s suite also reduce the crowding as measured by ADJSID from its start to its end. As already indicated in Example 1a, Mars begins with an imbrication of two 3–5[016]s that leaves a semitone between the pitch classes outside of their overlap. This SID of 1 leads to a rather low ADJSID of 0.55 because the average SID between two sets in the 3–5[016] set class is somewhat high: 1.83. Despite involving different set classes, an interpretation of imbrication affiliates Mars’s <G, D, D$$\flat$$, A$$\flat$$> opening (4–9[0167]) with the movement’s conclusion, which features repeated ffff hammer blows on a {C, A$$\flat$$, D$$\flat$$, G} chord (4–8[0156]). Referred to earlier as a fusion of tonic ({C, G}) and Neapolitan ({D$$\flat$$, A$$\flat$$}) harmonies, Mars’s final chord can also be deconstructed as two overlapping 3–5[016] sets: {C, D$$\flat$$, G} and {D$$\flat$$, G, A$$\flat$$}. The SID of this overlap is 4, the interval class of the C and A$$\flat$$, the two pitch classes outside of the overlap. This SID of 4 is much higher than the beginning’s SID of 1, and leads to a much more spacious ADJSID of 2.18 for Mars’s conclusion.²⁸ This higher ADJSID is the endpoint of the left thin arrow in Example 3. How could these discordant blasts coexist with ample personal space? One answer, following from the movement’s basic character, is that this juxtaposition models the achievement of such a space forcefully by pushing or striding away from congestion, an understandable precursor to more amicable solutions like a soundproof room. Another answer is that this juxtaposition parallels the augury of “endless bliss” from the aforementioned reference to the tonic-Neapolitan combination in Holst’s Psalm 86.

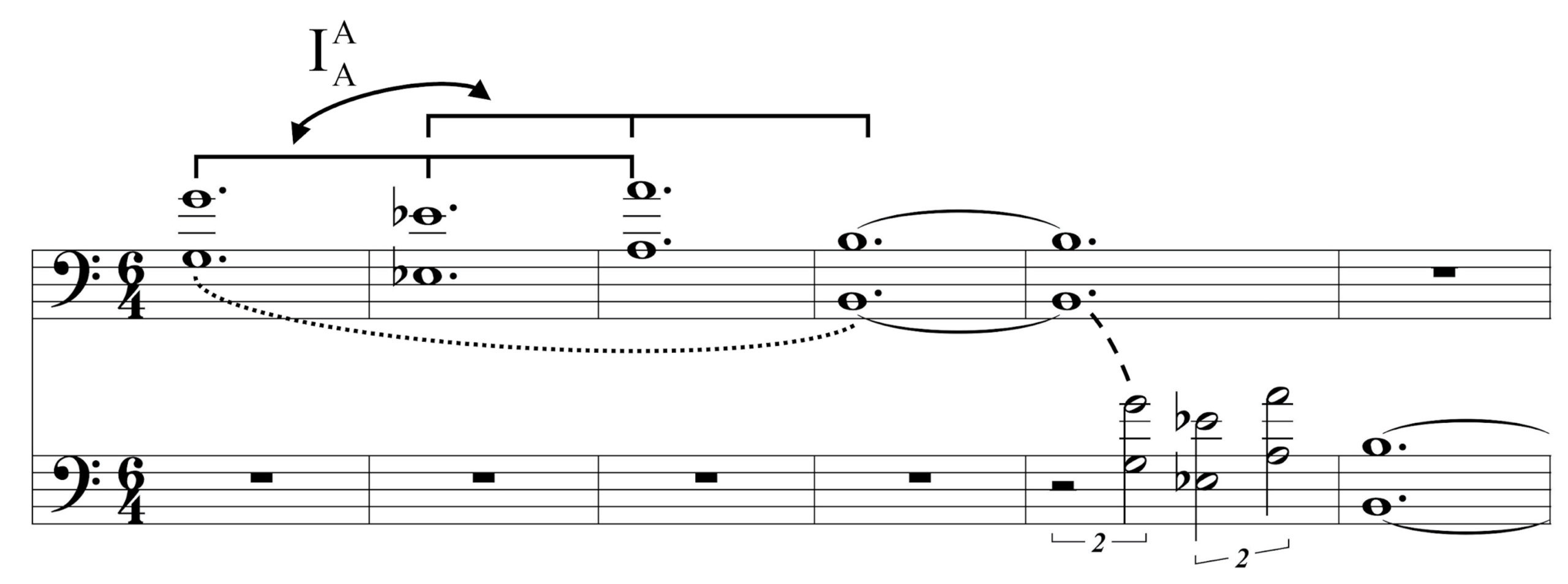
Example 5 shows Neptune’s opening in reduction. The first harmonic combination of trichords occurs in measure 3, as two 3–11[037]s—a G$$\sharp$$-minor triad in the treble, and an A-minor triad in the bass—coincide as two halves of a bichord. The second, in measure 7, is very similar, but the A-minor triad is replaced with a C-major triad. Since the two trichords of each bichord do not overlap in terms of pitch content, and, for each, the smallest unordered pitch-class distance between a pitch class in each triad is a single semitone, each projects a SID value of 1. Since the two trichords of each belong to set class 3–11[037], which has a AVGSID of 1.09, this opening projects an ADJSID of 0.92, which is the same as that of Venus and Mercury. This is well below the ADJSID of 1.83 of Neptune’s fadeout; thus, the entire suite’s progression from more to less crowded also unfolds within its final movement, as diagrammed with the right thin arrow in Example 3.

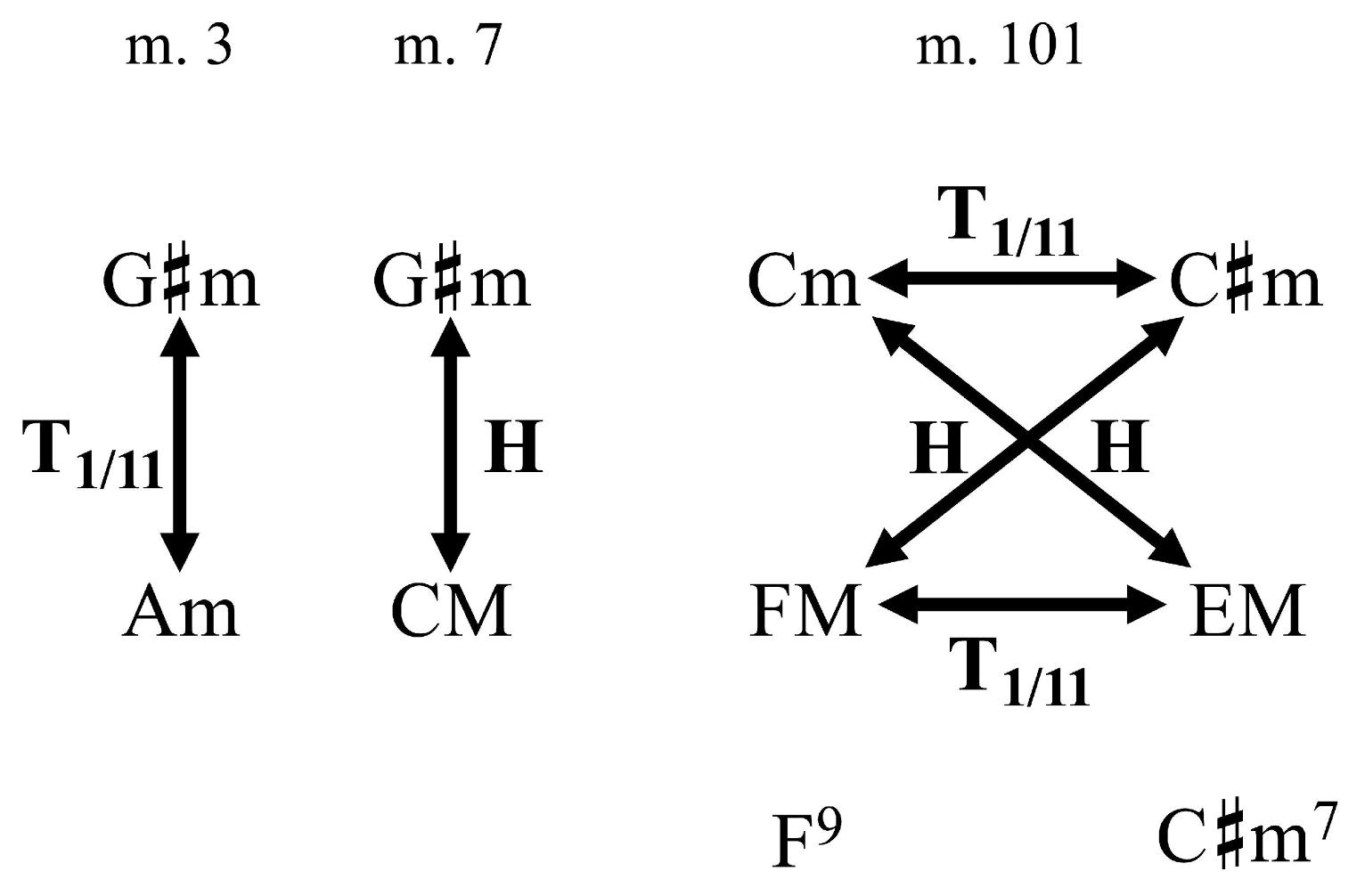
But Neptune’s bookends offer more than this. Just as the opening and closing of Mars features a rearrangement of strikingly similar pitch-class and trichordal-set-class materials to produce very different ADJSID results, Neptune does much the same, especially if one elaborates upon the SID metric. Example 6 compares the combinations of two triads of Neptune’s beginning with those of its conclusion. Representing the beginning are the two previously cited bichordal combinations; in the first, the combination may simply be called T_1/11, which refers to the unordered half-step transposition between the triads, and, in the second, the combination may be called a hexatonic-pole relation, or H (Cohn 1996). These two pairs of 3–11[037]s are two of many combinations with a SID of 1, and an ADJSID of 0.92; the latter symbolizes an uncomfortable interpersonal proximity that is nonetheless mostly expected given the closeness of most 3–11[037] pairs. However, these two triad pairs are the only two of the eighteen possible relations between two 3–11[037]s up to transposition, inversion, and temporal ordering that span the maximum number of three semitones between the triads in the pair. This exclusivity may also be seen in the mere three out of twenty-three triad pairs from Example 4 whose noteheads are all not black, representing three semitonal pairs that span the triads of each pair. (The difference of two out of eighteen versus three out of twenty-three reflects a difference in whether temporal ordering participates in the creation of equivalence classes or not.)

Stephen Soderberg (1998) formalized a measure #ic1(X, Y), which measures the number of pitch-class pairs—one pitch class from X and one from Y—that span the interval class 1.²⁹ Regarding the triadic combinations at the beginning of Neptune, both #ic1(G$$\sharp$$m, Am) and #ic1(G$$\sharp$$m, CM) equal 3, and no other triadic combination that is not a transposition, inversion, or retrograde of one of these two progressions has such a high number. Whereas SID measures how close one distinct part of a set is to one distinct part of another set, #ic1 measures how close (how semitonal-proximal in particular) all distinct parts of one set are to all parts of another set. Whereas a SID of 1, realized harmonically, analogizes at least the rubbing of elbows, an #ic1 of 3, realized harmonically, analogizes the entirety of one pressed up against the entirety of another, denying any part of either room to move or breathe.³⁰ This more comprehensive measure especially befits these two semitone-stuffed bichords from the beginning of Neptune. Despite their soft volume, they are arguably the two most dissonant bichords in the entire suite, even more so than the tonic-Neapolitan clash that ends Mars, because complete triads are only used in the former.³¹ However, additionally they represent a return not only to urban density after the last three movements’ relatively spacious SID of 2, but, as measured with #ic1, also to urban density’s most uncomfortably constrictive form.³²

In this context, the two fadeout chords are all the more palliative. Example 6 shows that the same two triad-pair types that return a #ic1 of 3—T_1/11 and H—are also present among the fadeout, but here their relation is realized exclusively horizontally instead of vertically. In the fadeout, the maximally abrasive semitonal harmony of Neptune’s opening becomes maximally effortless semitonal voice leading of Neptune’s ending. The isography of the beginning and ending, along with the ninety-degree turn from bichord to chord progression, feels particularly technological in the way it both reroutes and negates exactly the earlier grating dissonances. This canceling effect of Neptune’s fadeout, combined with the highest ADJSID scores for a 3–11[037] combination that the F⁹ and C$$\sharp$$m7 chords achieve, suitably signifies—not only with the waning volume of the moment but also in the context of the final movement’s and entire suite’s pitch content—the moment of leaving behind the noisy jostling of society, closing the door to a soundproof room, and, in the quiet solitude, achieving peace.

Conclusions

Holst recorded his “mood pictures” at each stage of the interplanetary odyssey, and one can posit the evolution of his “soul-states” over the course of his musical peregrination.³³ Holst broke the astronomical ordering of planets and placed Mars first because he wanted to depict what he was escaping. Mercury was originally annotated as “no. 1” in his sketch notebook, marking Mercury’s position as the first planet (from the Sun) in our solar system; but Mercury is not the starting point of the suite because Holst wasn’t beginning his journey from a place of frivolous, mercurial scherzo. He began from a state of agitated crowdedness in Mars and ends in a state of serene spaciousness by Neptune. The music progresses from cramped closeness to expansive personal (pc-set) space, just as the traveler traverses exoterically from the densest to the most rarefied reaches of the solar system, and esoterically from this world to the next.

Ours is not the first esoteric narrative to be found within The Planets, as Richard Greene saw in the music a “moral struggle” between “negative” atonality and “positive” tonality, in which a person must progress from the “primal” tonal “instability” of Mars to the “metaphysical” “fulfillment” of Neptune, in order to be “save[d]” (1995, 46, 42–43, and 66, respectively). Greene depicts this “philosophical journey” in somewhat religious terms, describing “the musical problem” of Mars as “an inner struggle, a trial by fire, a personal ordeal” (1995, 44, 41, and 47, respectively).

For a reclusive nature like Holst’s, the strain of a thriving, active career was a heavy burden, and the constant clamor of colleagues and students and admirers overtaxed his sensitive nerves. This, combined with his love of travel, his belief in mysticism, and his fascination with science, made the idea of a one-way vacation into outer space a most appealing fantasy for Holst. But The Planets has a dual function as an exoteric, physical journey into the solar system as well as an esoteric, metaphysical journey into heaven. This may explain why he detested incomplete performances of The Planets, and why he especially chafed at ending with Jupiter; for Holst, this would have been the equivalent of ending in purgatory. Like the five-day walking expedition that led to his Thaxted cottage, Holst painstakingly planned this seven-movement expedition to lead him Home.

---

References

Altman, Irwin. 1975. The Environment and Social Behavior: Privacy, Personal Space, Territory, Crowding. Monterey: Brooks/Cole.

Bax, Clifford. 1936. Ideas and People. London: Lovat Dickson Ltd. Publishers.

Clough, John. 1979. “Aspects of Diatonic Sets.” Journal of Music Theory 23 (1): 45–61.

Clough, John and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35 (1/2): 93–173.

Cohn, Richard. 1988. “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 10: 19–42.

—-. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music.” Perspectives of New Music 30 (2): 146–177.

—-. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15: 9–40.

Foucault, Michel. 1979. “What Is an Author?” In Textual Strategies, edited by Josue V. Harari, 141–160. Ithaca: Cornell University Press.

Ghuman, Nalini. 2014. Resonances of the Raj: India in the English Musical Imagination, 1897–1947. Oxford: Oxford University Press.

Greene, Richard. 1995. Holst: The Planets. Cambridge: Cambridge University Press.

Guerrero, Laura K. 2008. “Proxemics.” In The International Encyclopedia of Communication, 1st ed., edited by Wolfgang Donsbach. Malden, MA: Blackwell.

Hall, Edward T. 1966. The Hidden Dimension. Garden City: Anchor Books.

Hanegraaff, Wouter J. 2013. Western Esotericism: A Guide for the Perplexed. New York: Bloomsbury Publishing.

Head, Raymond. 1986. “Holst and India (I): ‘Maya’ to ‘Sita.’” TEMPO 158: 2–7.

—-. 1987. “Holst and India (II).” TEMPO 160: 27–36.

—-. 1988. “Holst and India (III).” TEMPO 166: 35–40.

—-. 1993. “Holst – Astrology and Modernism in ‘The Planets.’” TEMPO 187: 15–22.

—-. 2012. Gustav Holst and India. Self-published pamphlet. Chipping Norton: Sky Dance Press.

—-. 2014. Gustav Holst: The Planets Suite: New Light on a Famous Work. Self-published pamphlet. Chipping Norton: Sky Dance Press.

Hepokoski, James. 2006. “Framing Till Eulenspiegel.” 19th-Century Music 30 (1): 4–43.

—-. (1916) 1973. Sāvitri: An Episode from the Mahabharata, op. 25, rev. Imogen Holst. London: Faber Music. 

Holst, Imogen. 1958. Gustav Holst, a Biography. London: Oxford University Press.

—-. 1981. The Great Composers: Holst. London: Faber and Faber Limited.

Leo, Alan. (1913) 2003. What is a Horoscope and How is it Cast? Whitefish: Kessinger Publishing.

Matthews, Colin. 2000. “Sāvitri.” Liner notes for Holst: Sāvitri and The Dream-City. City of London Sinfonia, Richard Hickox, conductor, CDH55042. London: Hyperion Records.

Mitchell, Jon. 2001. A Comprehensive Biography of Composer Gustav Holst, With Correspondence and Diary Excerpts; Including His American Years. Lewiston: Edwin Mellen Press.

Moore, Allan F., Ruth Dockwray, and Patty Schmidt. 2009. “A Hermeneutics of Spatialization for Recorded Song.” Twentieth-century Music 6 (1): 81–112.

Morris, Robert. 1979–80. “A Similarity Measure for Pitch-Class Sets,” Perspectives of New Music 18 (2): 445–460.

Murphy, Scott. 2006. “The Major Tritone Progression in Recent Hollywood Science Fiction Films.” Music Theory Online 12 (2).

Nawijn, Jeroen, Miquelle A. Marchand, Ruut Veenhoven, and Ad J. Vingerhoets. 2010. “Vacationers Happier, but Most not Happier After a Holiday.” Applied Research in Quality of Life 5 (1): 35–47.

Nehamas, Alexander. 1986. “What an Author Is.” Journal of Philosophy 83: 685–691.

Scheer, Christopher M. 2020. “Gustav Holst’s Beni Mora and the Orientalist Imagination.” In The Symphonic Poem in Britain, 1850–1950, edited by Michael Allis and Paul Watt, 219–244. Woodbridge: Boydell Press.

Seidl, Arthur. 1913. Straußiana: Aufsätze zur Richard Strauß Frage aus drei Jahrzehnten. Regensburg: Gustav Bosse.

Shore, Bernard. 1949. Sixteen Symphonies. London: Longmans, Green and Co.

Short, Michael. 1990. Gustav Holst: The Man and His Music. New York: Oxford University Press.

Soderberg, Stephen. 1998. “The T-Hex Constellation.” Journal of Music Theory 42 (2): 207–218.

Straus, Joseph. 2021. “Music Theory’s Therapeutic Imperative and the Tyranny of the Normal.” Music Theory Spectrum 43 (2): 339–348.

Väisälä, Olli. 1999. “Concepts of Harmony and Prolongation in Schoenberg’s Op. 19/2.” Music Theory Spectrum 21 (2): 230–259.

Van Boven, Leaf and Laurence Ashworth. 2007. “Looking Forward, Looking Back: Anticipation Is More Evocative Than Retrospection.” Journal of Experimental Psychology: General 136 (2): 289–300.

Discography

Holst, Gustav. 1994. The Planets, with the Georgian Festival Orchestra, conducted by Jahni Mardjani. Infinity Digital, compact disc.

1. The “exoteric narrative” is the literal story line referenced in the programmatic title, which serves as a metaphor for the “esoteric narrative,” the figurative meaning beneath the surface (Seidl [1913, 57], cited in Hepokoski [2006, 14]). See Hanegraaff (2013) for a deep exploration of esotericism.
2. We have adapted this term from Richard Strauss’s subtitle of “Frei nach Fr. Nietzsche” (“freely after Nietzsche”) in describing the relationship of his Zarathustra to Nietzsche’s.
3. See Head (1993 and 2014) for detailed accounts of Holst’s interest in astrology.
4. Clifford Bax, who introduced Holst to astrology, claims that Holst lost interest in astrology after completing The Planets (Mitchell 2001, 119). Head (1993, 17) refutes this claim by citing Holst’s friendship with astrologer Vivian E. Robson, and her personal inscriptions to Holst in two of her books (housed at the Holst Birthplace Museum). Mitchell (2001, 130), on the other hand, confirms Imogen’s and Bax’s accounts, stating that “astrology had been the beginning [of The Planets], but only the beginning.” Similarly, Short (1990, 122) says that “Holst used the astrological connotations of the planets simply to give the mood of each movement, and then structured the resulting musical material according to his own principles.”
5. Holst wrote this in a letter to music critic Herbert Thompson, in which he refuted some of the common assumptions about the content of The Planets. From the Herbert Thompson Collection, The University of Leeds, Brotherton Library, MS 361/148, 23 July (1922). Cited in Greene (1995, 40).
6. So vehement was Holst’s distaste for social obligation and public interaction that later in life, he often remarked that success was the worst thing that ever happened to him. He wilted when approached by press or photographers (I. Holst 1981, 54), he shrank away from popularity and recognition, he hated coming onto stage to receive applause, and he declined all honorary degrees and titles.
7. He even learned Sanskrit well enough to translate his own texts. For more on Holst’s “Sanskrit period,” see Ghuman (2014) and Head (1986, 1987, 1988, and 2012).
8. In a similar vein, Head (1993) offers an interpretation of The Planets as an astrological horoscope that Holst cast for himself, with each planetary character having some specific meaning in his life.
9. And to quote Imogen Holst, “Mars was not a comment on the war: it was a prophecy” (1981, 48–49).
10. Shore equates these rough, driving rhythms with “the rude facts of existence and social responsibilities” (1949, 321–322).
11. The final movement of Vaughan Williams’s Sea Symphony is titled “Passage to India,” incidentally, which at once ties in with Holst’s Venus and Sāvitri. Vaughan Williams was Holst’s dearest friend, and the two held each other’s music in the very highest regard.
12. We are grateful to the reviewer who pointed out a similarity between this Mars=public / Venus=private dichotomy and the “First Dance” / “Second Dance” of Holst’s Beni Mora (1910). Scheer (2020) describes this dichotomy in Beni Mora, in which the “First Dance” depicts a bustling public space and the “Second Dance” depicts an intimate private space. Beni Mora is also a travel-based work, inspired by Holst’s trip to Algeria.
13. The so-called “double symphony” scheme entailed dividing up the seven movements of The Planets into two four-movement symphonies: Mars, Venus, Mercury, Jupiter and Jupiter, Saturn, Uranus, Neptune (Greene 1995, 24).
14. Shore describes this as a “creaking advance, serious if not yet terrible” (1949, 319).
15. This motivic incessancy is not unlike Berlioz’s idée fixe in his Symphonie Fantastique.
16. Most recordings substantially soften the blow of this measure to a more bearable fff level. For the full, awful effect Holst notated in his score, we recommend the following obscure recording: Gustav Holst, The Planets, with the Georgian Festival Orchestra, conducted by Jahni Mardjani, recorded 1994, Infinity Digital, compact disc.
17. If the mood is slightly less sanguine than before (in Saturn), it is because death is now being faced, rather than floating as an abstraction in the future.
18. Debussy’s wordless sirens in Nocturnes come to mind.
19. We thank the reviewer who drew our attention to this connection.
20. Holst held differing conceptions of the afterlife at various points in his life. See Ghuman 2014 (143–150) for a discussion of Holst’s exploration of devachan, the theosophical concept of afterlife, in several of his compositions, including the Saturn movement of The Planets.
21. Imogen (1981, 51) gives a detailed account of the procedure: “The singers began by standing out of sight in a box next to the Queen’s Hall organ. They were able to look at the conductor through a narrow gap between the curtains. After about three bars they slowly turned round and walked down a corridor, watching the beat of a sub-conductor, who led them into a room at the far end, where a door was open to receive them. They walked the whole length of this room while someone gradually closed the door, and they went on singing until the applause of the audience told them that their voices were no longer audible. Holst used to make them rehearse this over and over again: any shoes that squeaked had to be taken off, and the door had to be shut absolutely silently.”
22. For example, theorists have recognized significant patterns in certain works of Mozart using tonally indifferent sets either diatonic (Clough 1979) or chromatic (Straus 2021).
23. “Transformational combination” is a generalization of “transpositional combination”; see Cohn (1988).
24. Within the disciplines of musicology and music theory, popular music scholarship has been a recurrent locus for the integration of proxemics research, such as Moore et al. (2009).
25. This summary of Altman’s distinction follows that of Guerrero (2008).
26. This imperial metaphor captures many different aspects of this model, including the circularity of the space, the specific diffuse distribution of a 3–11[037]’s membership, the multiplicity of the 3–11[037] set class’s membership, the considerable entanglements of this membership because of this diffuse distribution, and geopolitical friction between neighbors as analogous to interpersonal friction between proximal strangers.
27. This succession from SID to ADJSID is similar to the succession from SIM to ASIM in Morris (1979–80), as well as the succession from EMB to ADJEMB in Cohn (1992), among others.
28. Another generation of {C, A$$\flat$$, D$$\flat$$, G} by transformational combination is with overlapping 3–4[015]s: {G, A$$\flat$$, C} and {A$$\flat$$, C, D$$\flat$$}. This produces a SID of 6, the maximum for this and any trichordal combination.
29. Soderberg (1998) generalizes this measure (#ici) for all seven interval classes, including zero.
30. Although #ic1 provides a higher degree of precision about the semitonal relationship between two sets than SID, SID attends to how far apart the two sets’ closest members are, which #ic1 does not. Therefore, each measure contributes information about two sets’ mutual proximity that the other does not.
31. Furthermore, the use of a complete tonic-Neapolitan bichord at the end of Mars, such as {G, A$$\flat$$, B($$\flat$$) , C, D, E$$\flat$$}, would have denied the movement’s passage from more to less crowded as previously proposed.
32. However, according to Väisälä (1999), both of these bichords could be more dissonant if their two constituent triads were swapped in register, because then the majority of semitones in each bichord would be realized as minor ninths instead of major sevenths. Nonetheless, the perspective adopted in our analysis ignores registral differences.
33. “Soul-states” or Seelenzustände, as both Robert Schumann and A.B. Marx understood it, were deep feelings into which certain musical expressions could tap, transcending a simplistic mapping to basic signifieds (like astrological or astronomical planets, or mythological characters).