Unveiling the Signifiers of Rain in John Adams’s China Gates

Leah Amarosa

Abstract

While previous scholarship has focused on the close relationship between John Adams’s pieces, China Gates and Phrygian Gates, this paper offers an alternative interpretation of China Gates based on Adams’s recent revelation that the piece was inspired by an endless winter rainstorm that beat down on his cottage. This paper utilizes a two-part methodology: musical elements are analyzed first using theoretical tools, after which I adopt a semiotic framework based on cognitive theories of cross-domain conceptual blending to demonstrate how these musical elements signify rain through symmetry, phasing, parsimonious voice-leading, as well as pitch-class and set-class repetition. In this paper, I unveil the analogical processes by which the physical phenomenon of rain is represented by musical features and illustrate the action of cross-domain mapping in constructing a conceptual blend. I argue that in producing a sonic analog for rain, China Gates suggests a narrative tension between consistency and dynamism.
View PDF
Return to Volume 36

Keywords and Phrases: Semiotics; cognition; minimalism; symmetry; voice leading

Introduction

“Musical semiotics begins from the premise that music [like all cultural creations] is a signifying phenomenon” (Tarasti 2016, 48). In some cases, the composer suggests a meaning through a title or performance note. Other times, the interpretation is left to the performer, listener, or analyst. In what John Adams considers his “opus one,” he gives solo piano pieces Phrygian Gates and China Gates varying levels of explanation regarding meaning (n.d.). On his website, Adams provides a lengthy description of Phrygian Gates, while China Gates receives just a few short sentences. For this reason, many scholars have analyzed the meaning of China Gates with respect to Phrygian Gates, focusing on each title’s relationship to gating in electronic machines and waveforms (see Behar 2014; Escuder 2012; Lankov 2014). However, while working with the Los Angeles Philharmonic, Adams shared a video in which he describes the inspiration for China Gates. In this video, Adams reveals his inspiration: the repetitive, rhythmic patterns of “endless winter rain” that beat down on his little cottage in San Francisco in 1977 (LA Phil 2020). In this paper, I will demonstrate various musical elements in this piece that signify rain, including symmetry, phasing, voice leading parsimony, as well as pitch-class and set-class repetition. Thus, my research attempts to provide an alternative to interpreting China Gates within the framework of the electronic medium (gating), and instead interpret the piece through a naturalistic lens, in which musical and physical domains combine to construct meaning.

1. Methodology

This paper combines methodologies applied by other scholars in music theory concerning minimalist techniques, especially in works by John Adams. I primarily build on Alexander Sanchez-Behar (2014, 46–60) by discussing further layers of symmetry in China Gates, such as beat-class set symmetry, and consider that these symmetries communicate signify elements of rain. In addition, I apply ideas related to musical signifiers in minimalist compositions from scholars such as Sean Atkinson and Rebecca Leydon. My research stems from the work of Atkinson (2011), which observes that repetition and variation of motives in the music of Steve Reich have extramusical meaning. I apply this idea further to John Adams’s China Gates. Furthermore, Leydon (2002) discusses the different effects of repetition in minimalist works. I continue this conversation with the proposition that repetition in China Gates signifies constant rain.

This paper’s semiotic framework is based on cognitive theories of cross-domain conceptual blending, pioneered by linguists Gilles Fauconnier and Mark Turner (1995, 1998), and applied to music soon after by Lawrence Zbikowski (1997, 2002). Zbikowski’s research contends that meaning construction in music is dependent on mappings between musical domains and other conceptual domains such as image, text, or color. A conceptual blend arises when two musical and extramusical domains are blended, cognitively informing the listener’s understanding of the music.

Two key concepts are necessary here – metaphor and analogy. Following George Lakoff’s (1993) definition, Zbikowski understands metaphor as “a basic structure of understanding through which we conceptualize one domain (the target domain, which is typically unfamiliar or abstract) in terms of another (the source domain, which is most often familiar and concrete),” meaning that metaphor is a significant part of the human experience, but is inherently asymmetrical (2002, 66). Zbikowski’s more recent research has shifted towards analogical mapping, in part due to his view that analogy is a stronger relationship than metaphor, arguing that “it is not simply about correlating elements from one domain with elements in another domain, but about mapping relationships between these domains” (2017, 29).

In my analysis of the signifiers of rain in China Gates, I adopt Zbikowski’s framework for analogy, demonstrating how various musical elements analogically correspond with aspects of rain to create a conceptual blend. To elucidate these signifier-signified relationships, I will employ the conceptual integration network (CIN), a model developed by Fauconnier and Turner (1998), applied extensively in Zbikowski’s “Foundations of Musical Grammar” (2017) in the context of analogical mappings. In a CIN, each conceptual domain creates its own “mental space” with distinct characteristics. Thus, a CIN explicitly unveils the connections that result in conceptual blending; in this case, it will show how the physical phenomenon of rain is represented by a musical element, and how these domains interact to create meaning. Through this methodology, grounded in musical semiotics and cognition and deepened through music-theoretical tools, I unveil the musical signifiers that create a “sonic analog” for rain.¹

2. Preliminary Information

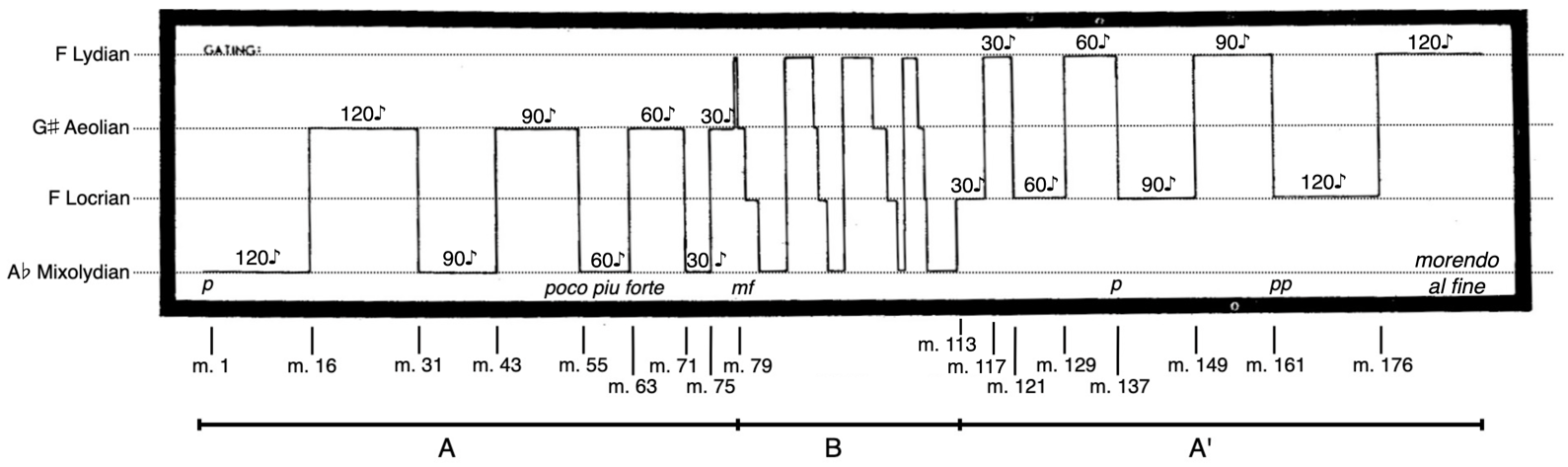
China Gates was written as a companion piece to the much longer piece, Phrygian Gates. Both pieces exhibit many features of musical minimalism, including simple patterns and gradual changes. However, in these pieces, Adams claims to have discovered something new: “I was already searching for ways to convolute and enrich the inherent simplicities of the style” (n.d.). This is exemplified in what I call the “simple complexities” of China Gates. That is, although Adams describes the piece as delicate and gentle, it is the intricate compositional devices hidden beneath the surface that bring about that perception. China Gates has a tripartite structure, yet is further broken down into “gates,” a term borrowed from electronics, described by Adams as “the moments when the modes abruptly and without warning shift” (n.d.). In addition to change of mode, a new gate also introduces new textural and rhythmic layers. The piece consists of three voices: a pedal tone held throughout the A sections of the piece, a steady eighth-note pattern in the right hand, and various rhythmic patterns that expand and contract over the course of each gate in the left hand. In the performance notes, Adams provides a gating diagram, displayed in Figure 1, to which I add measure numbers, dynamics, form, and modes (1983). The symmetrical construction of this form, apparent by the shape of the diagram, will be the focus of the next section.

3. Symmetry

Symmetry is one of the unifying features of the piece, occurring in form, articulation, rhythm, and texture. In this section, I analyze the various symmetrical features of the piece, and then illustrate how the musical elements signify the physical elements of rain, constructing meaning through cross-domain mapping and conceptual blending. The gating diagram in Figure 1 presents a clear macro-layer of symmetry: the length of the gates. More specifically, in the A sections, the number of eighth-note durations in each pair of gates mirrors the length of the corresponding gates in the other A section. In fact, Adams describes the piece as “an almost perfect palindrome” (1983). The piece is also nearly symmetrical in dynamic intensity. The A section begins at p and then crescendos into the B section, which has a dynamic level of mf. 23 measures into the A’ section, the dynamic level lowers to p, quiets to pp at m. 161, and the music gradually dissipates through the end of the piece, marked morendo al fine (lit. “dying to the end”).

Symmetry also occurs in the rhythm and texture of China Gates. At the macro level, symmetry is exhibited as the rhythm and texture suddenly shift at the beginning of each new section. The rumbling bass pedal unexpectedly vanishes at the start of the B section, then reenters at the start of the A’ section. And while the right hand continues with a steady eighth note pattern throughout the whole piece, the left hand exhibits a contracting and expanding pattern throughout the A sections, then joins the left hand in the steady eighth note pattern in the B section. Examples 1a and 1b display this shift between each section.

Furthermore, symmetry in rhythmic displacement, or phasing, contributes to the palindromic structure of the work. Rhythmic irregularity and complexity arise through phasing, a compositional device that Steve Reich pioneered in Come Out (1966) with tape loops, and later utilized in works such as Piano Phase. In Piano Phase, the phasing technique is achieved through two pianos playing short identical motives, where one pianist keeps a steady tempo and the other increases their tempo until they slowly become out of phase with one another. In China Gates, the pianist’s hands each play a different rhythmic motive, with phasing occurring when the motive in one hand increases or decreases its length to a value that is not a multiple of the other hand. In other words, the phasing arises from differences in motive length between the two hands, rather than differences in tempo.

For instance, in the first fifteen measures (the first gate), the left hand undergoes various transformations in motivic length. Example 2 presents the motivic length of each hand, with annotations showing where the hands sound “in phase” and “out of phase.” At the beginning of the piece, each motive has a length of seven eighth notes. Over the course of the gate, the left-hand motive shifts between lengths of four, six, seven, and eight eighth-note lengths. Any time the motives are not the same length, nor a multiple of the other, they are out of phase.

While phasing in itself is a dynamic process with several cognitive implications, phasing in China Gates also occurs symmetrically between the gates. To reveal this symmetry, I apply beat-class set theory.³ While the right-hand motive is always of the same length in each gate, the left hand’s adjustments in length cause a shifting metrical cycle. The metrical cycle for each motive is the number of eighth-note pulses it contains. Table 1 shows the beat-class (bc) sets of the first two gates. An X indicates an attack on an eighth note, and the middle horizontal line represents the axis of symmetry, which corresponds to the gate change (motives 1–6 occur in the A section, 7–12 in the B section). Finally, the gray boxes indicate that the motive does not have an attack on that eighth-note unit. For example, whereas the length of motive #5 is eight eighth-note pulses, with attacks on <1,3,5> (already ordered) resulting in prime form [024], the modular system of motive #1 is seven eighth-note pulses in length. Therefore, {1,3,6} is not ordered and must first be ordered to <6,1,3> to find the prime form [024]. This table reveals perfect symmetry in bc sets between these two gates. Moreover, every bc set is [024] except for those directly preceding and succeeding the axis of symmetry. However, this differing bc set is connected through a subset relationship, as [02] is a subset of [024]. This symmetric structure occurs between all successive gates in the A sections of the piece, extending the overall symmetric structure of the work.

Motive #	Eighth-Note Beat								Beat-Class Set
	1	2	3	4	5	6	7	8
#1	X		X			X			[024]
#2	X		X		X				[024]
#3	X		X			X			[024]
#4	X		X		X				[024]
#5	X		X		X				[024]
#6	X		X						[02]
#7	X		X						[02]
#8	X				X		X		[024]
#9	X		X		X				[024]
#10	X		X			X			[024]
#11	X		X		X				[024]
#12	X			X		X			[024]

 The various layers of symmetry in this piece create multiple structural correlations between the musical domain and the conceptual domain associated with rain. On the macro level, the formal symmetry of the piece is analogous to the process of a rainstorm, establishing a narrative through the blending of these domains.⁴ The UCAR Center for Science Education describes storms as having three stages: the developing stage, the mature stage, and the dissipating stage (UCAR n.d.). The developing stage, when the storm clouds are formed, is signified by the A section with the quiet dynamic level; the bass pedal may even evoke the sound of quiet thunder drawing near. The second stage, the mature stage, is when the storm gains energy and reaches its peak. In China Gates, this is represented by the B section, which exhibits a louder dynamic and more rhythmic energy. The last stage, called the dissipating stage, is when the storm weakens and dies out. In China Gates, the A’ section similarly fades way, its musical elements marking a return to normalcy.

On the micro level, rain is represented through mimesis. The eighth-note consistency throughout the entire piece in the right hand mimics the repetitive, steady sound of rain. Secondly, irregularity arising from phasing signifies the organic source of Adams’s inspiration. Despite shifts between modes, the beat-class symmetry suggests continuity. Thus, there is a paradoxical aspect to this piece, as there is to rain: there is a stability in process, yet a shift in energy, creating a novel narrative from the blending of the two domains.

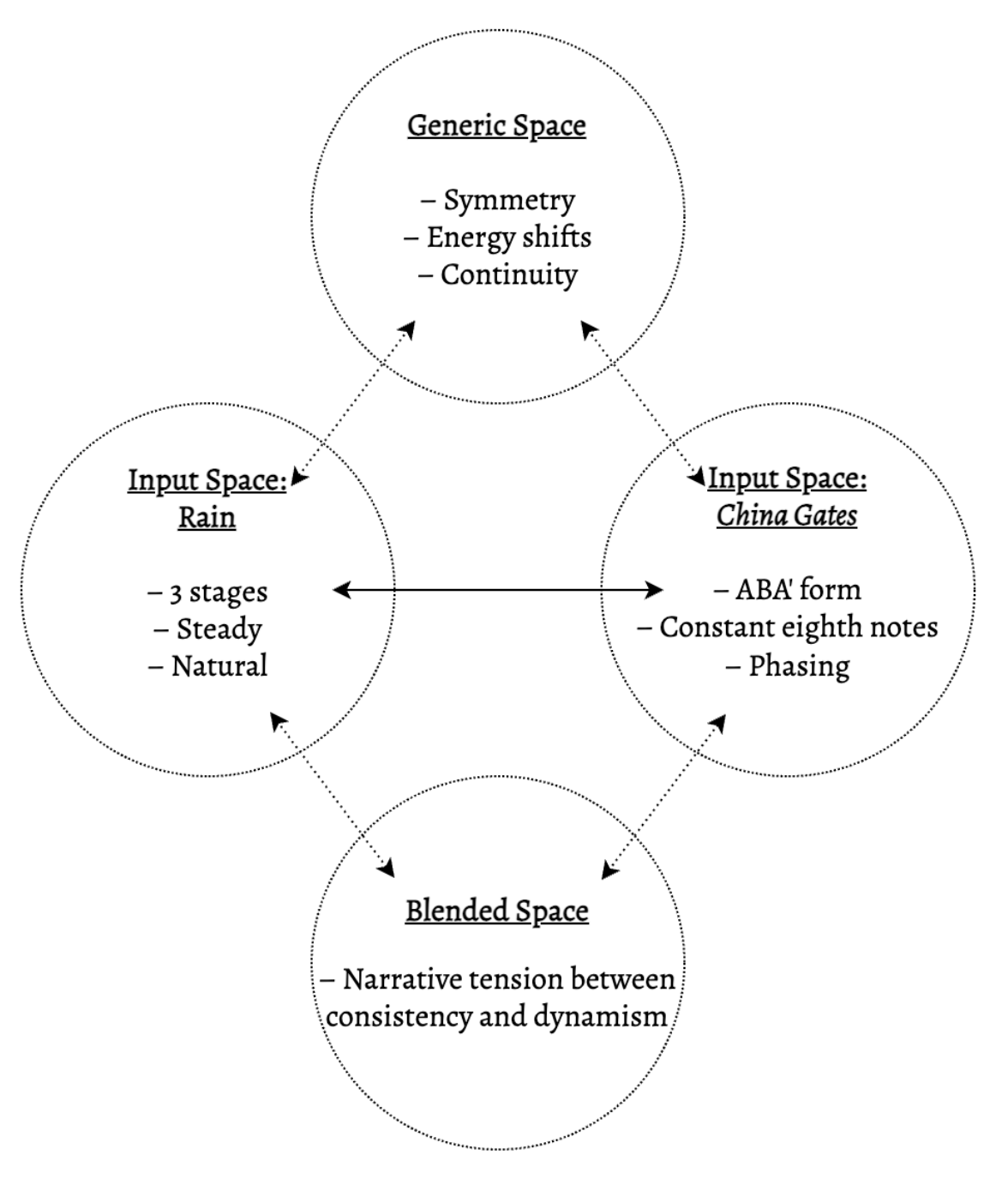
The conceptual integration network (CIN) for these large-scale processes is featured in Figure 2. Recall that a CIN is constructed from different mental spaces. The two mental spaces activated by this work are the musical space and John Adams’s comment about the piece’s inspiration; these are called input spaces. At the top of the diagram is a generic space, which “captures the abstract core idea shared between the two correlated spaces” (Zbikowski 2017, 49). Lastly, these three core spaces activate the fourth space, referred to as the blended space. This conceptual blend creates a new idea out of the analogical mappings– that the musical work exhibits a narrative tension between consistency and dynamism.

4. Pitch Classes and Voice Leading

Thus far, this analysis has focused on large-scale form and rhythm. Next, I identify how the pitch classes and voice leading achieve continuity and unity through the contrasting sections, signifying the endlessness of rain. In this section, the theoretical approaches of both pitch-class set theory and neo-Riemannian theory will elucidate the relationship between the motivic movement of this piece and the environmental forces of rain, resulting in a conceptual blend. First, this piece is based on a limited number of pitch-class collections. As a result, there is not only repetition of rhythmic patterns, but also pitch-class patterns. In China Gates, the A sections consist of two alternating modes, with changes of mode coinciding with each new gate. One major and one minor mode (according to the scalar third) belong to each section. In the A section, the alternation is between A$$\flat$$ Mixolydian and G$$\sharp$$ Aeolian. Because the tonic of each mode is the same pitch class (pc), the A$$\flat$$/G$$\sharp$$ pedal persists throughout the entire section. Likewise, the A’ section alternates between F Locrian and F Lydian, with an F pedal throughout most of this section. The utilization of these modes is significant in achieving pitch-class repetition in this piece. In the A section, the only difference in pc content between A$$\flat$$ Mixolydian and G$$\sharp$$ Aeolian is between the third and sixth scale degree of each mode, consistent with a hearing of the modes as major or minor, respectively. However, in the A’ section, F Locrian and F Lydian have only two pcs in common: their tonic and C$$\flat$$/B. As a result, the first section has two pcs not in common, while the last section has only two pcs in common. Furthermore, these are the same pcs: in the A section, the differing pcs are B/C and F/E, while in the A’ section, the common pcs are B and F.

In discussing continuity, or endlessness, another pitch-class link in the piece occurs in the modes of the A sections. G$$\sharp$$ Aeolian (A) and F Locrian (A’) contain nearly the same pcs.⁵ However, the most significant feature of the pitch-class collections in this piece is the alternation between the paired major and minor modes. Adams states, “It strikes me now as a piece calling for real attention to details of dark, light and the shadows that exist between” (Adams n.d.). These two contrasting features, dark and light, are also representative of rain. On the one hand, a rainstorm creates darkness, dreariness, and even gloom. But on the other hand, rain is necessary for the growth and regeneration of life. Thus, altering just two pcs leads to both conflict and continuity simultaneously, evoking the same blended space as in Figure 2.

Further continuity is displayed in the relationships between set classes which heavily gravitate towards common tone preservation in their transformations. Within each gate in the piece, each hand plays a repetitive pattern consisting of between two and six pitch classes. Adams deals with these transitions with “extreme delicacy” through common tones and parsimonious voice leading (Adams n.d.). Although the gates oscillate dramatically between major and minor modes, each hand’s pitch collections maintain at least one common tone when moving from one gate to the next. These pitch-class sets are often further related through transposition, inversion, or triadic transformation. Additionally, the pitch classes that are not common tones often create semitonal voice leading. These relationships produce smooth voice leading and transitions, producing a sound characteristic of a steady rainstorm. To illustrate these transformations, I will apply a combination of pitch-class set theory and neo-Riemannian theory.

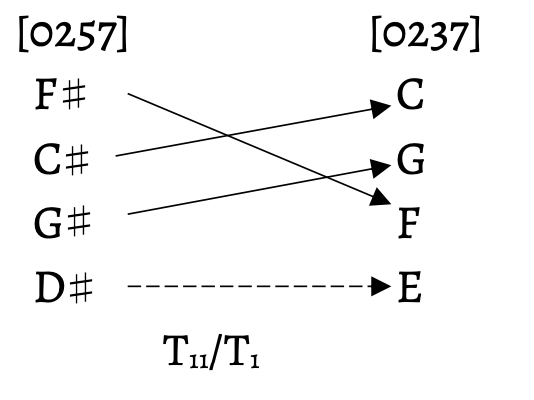
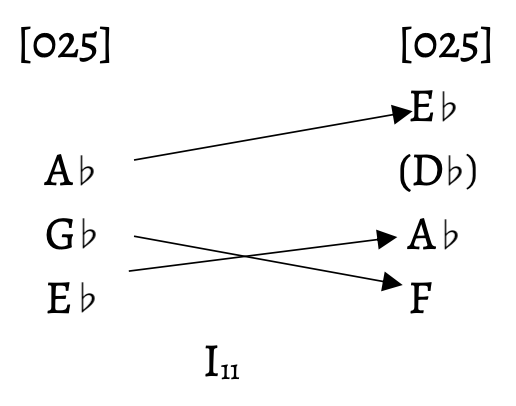
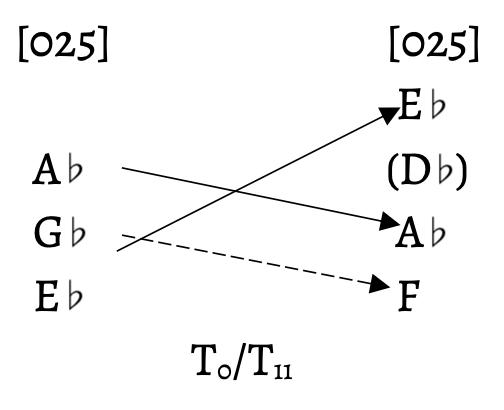
At the macro level, the transitions between formal sections in the piece are smooth in voice leading and harmony, connected by set classes that relate through transposition, inversion, or inclusion. Although there are changes of mode and key signature, these relationships provide a sense of continuity and flow through these transitions. In this way, mm. 75–78 set up the B section of the piece. The right-hand motive is of set-class 4–23[0257], moving to set-class 4–14[0237] in m. 79. This voice leading is best reflected using Shaugn O’Donnell’s dual transposition model (2007). Figure 3 displays this dual transpositional voice leading; note that each voice moves by half step, either down (T₁₁) or up (T₁). The left-hand motives interact similarly. Including the G$$\sharp$$ pedal in the bass, the left hand in mm. 75–78 is also of set-class 4–23[0257], which moves to set-class 4–14[0237] in m. 79. Figure 4 shows this dual transpositional voice leading; all voices also move by semitone. Finally, the last two notes sounded together in the A section create a perfect fifth, and the first harmony of the B section is also a perfect fifth, creating parallel octaves by ascending semitone (refer back to Example 1a). Through these various connections, the A section moves smoothly into the B section.

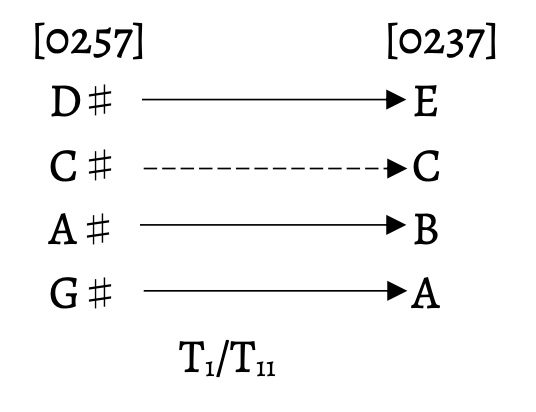
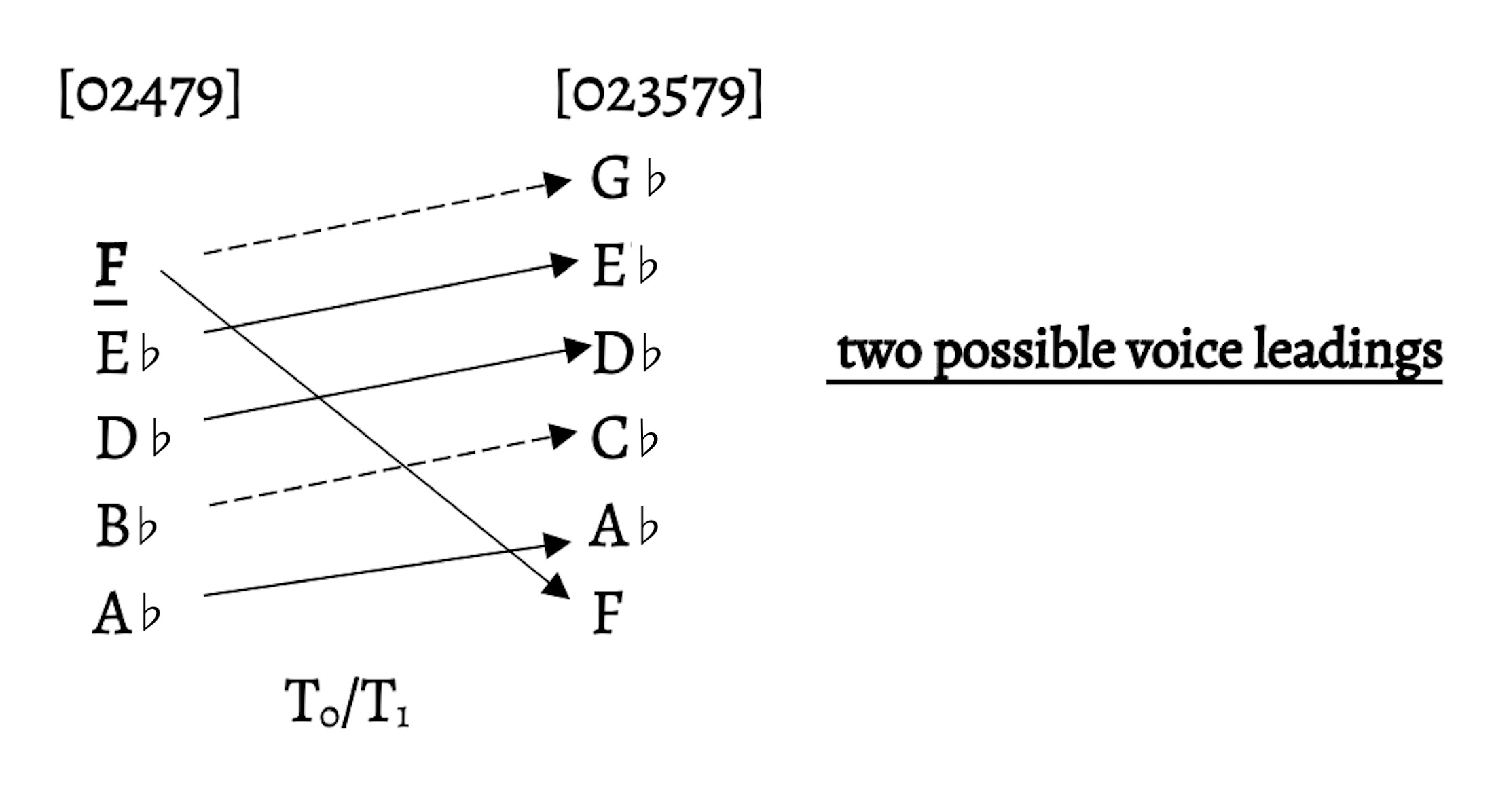
Likewise, the shift from the B section to the A’ section exhibits many of the same relationships. The right-hand motive in mm. 109–112 is of set-class 3–7[025], which transitions into m. 113, the start of the A^‘ section. The set class of the right hand in mm. 113–116 is 4–22[0247]; however, I will consider the statement of the motive that contains three pitches of set-class 3–7[025], the same as the final set class of the B section. If one were to use voice-leading transformations to connect these two set classes, the result would be mapping at I₁₁ (see Figure 5a). However, this mapping does not consider the common tones in these pitch classes. Figure 5b demonstrates how dual transpositions reflect this voice leading accurately. The left hand, in contrast, features much longer motives between these two sections. In mm. 109–112, the five-note motive is of set-class 5–35[02479], the pentatonic collection. The beginning of the A^‘ section features a six-note motive, set-class 6–33[023579]. Both motives have four pitch classes in common; this smooth voice leading emerges in the dual transpositions shown in Figure 6. These close relationships, in which voices either stay common or move by semitone, establish continuity between the contrasting sections of the piece, analogous to the continuous downpour of rain.

Not only is continuity reflected in the section transitions, but also between each gate through interval preservation. At the macro level, the left hand of each pair of gates is a mirror inversion of intervals of the other. Sanchez-Behar describes this phenomenon as “step-class retrograde inversion” (2016, 50). In other words, the ordered pitch intervals (opis) are symmetric in each pair of gates. Example 3 displays this relationship between two adjacent gates in mm. 71–78. This symmetry occurs in each pair of gates in the A sections. Although these pairs of gates are in different modes and key signatures, the left-hand intervals remain symmetrically equal. The right-hand melodies are not as systematic. However, typically an opi is preserved between each gate. Examples 4a–c present an occurrence of this event from each section.

Additionally, at the micro level, many of the gates in the A and B sections can be connected through smooth triadic transformations:  neo-Riemannian operations P, L, and R. Timothy Johnson has applied this same technique to analyze triadic sections in Adams’s Nixon in China (2011), and Joseph Straus in Adams’s Harmonium (2016, 191–192). These triadic transformations preserve common tones and create parsimonious voice leading. The first example in China Gates appears in mm. 15–16. The last three pitch classes of the right-hand motive of the first gate are E$$\flat$$, A$$\flat$$, and C, creating an A$$\flat$$-major triad (A$$\flat$$+). Then, the first three pitches of the right hand in the second gate are D$$\sharp$$, G$$\sharp$$, and B, a G$$\sharp$$-minor triad (G$$\sharp$$–). These triads are related by a P (parallel) transformation, shown in Example 5. From the second to the third gate, the P transformation is performed again, undoing the transformation. Next, from the third to the fourth gate, the A$$\flat$$-major triad in the right hand shifts to a B-major triad. These triads, which have one common tone, E$$\flat$$/D$$\sharp$$, can be related with a PR transformation, as shown in Example 6. In this example, one voice moves by one semitone, and the other moves by two semitones, which still creates parsimonious voice leading. Like the first transformation, this one is undone in the next gate.

The gate transitions in the B section also exhibit parsimonious voice leading. In m. 80, the right hand arpeggiates a B-major triad. In m. 81, one pitch is moved by a semitone, forming an arpeggiated E$$\flat$$-minor triad. These triads relate through an L transformation, where the B-major triad is inverted around its minor third. Superset or subset relationships connect many of the motives that are not related by neo-Riemannian transformations. Table 2 displays a complete map of the set-class sequence in the B section. Nearly all the set classes relate to the concurrent set or a set in the previous or next measure by repetition, subset, or superset.

	m. 79	m. 80	mm. 81–82	mm. 83–86	mm. 87–90	m. 91	m. 92	mm. 93–95	mm. 96–99	mm. 100–101
Right Hand	(0237)	(037)	(037)	(0247)	(0135)	(037)	(027)	(025)	(0157)	(01)
Left Hand	(0237)	(015)	(0135)	(0135)	(0135)	(0235)	(0246)	(03)	(0156)	(0247)

	m. 102	m. 103	m. 104	mm. 105–106	m. 107	m. 108	mm. 109–112
Right Hand	(02)	(02)	(05)	(05)	(013)	(013)	(025)
Left Hand	(0235)	(024)	(05)	(01568)	(0235)	(013)	(02479)

Thus, the pitch-class collections, motives, set classes, and their transformations exhibit cohesion throughout both large-scale formal sections and between gates, signifying the constant, gentle rain. The consistency of processes over various changes of mode and register demonstrates Adams’s commitment to a cohesive sound. Adams’s own words reveal this commitment: “I remember hearing the rain coming down incessantly on the roof of this little cottage and there’s something about the gentle, repetitive patterns of this piece that I connect with that experience” (LA Phil 2020). Even through the dramatic shifts between major and minor and the contrasting formal sections, there is a unified sound. For this reason, I assert that this cross-domain mapping between the physical phenomena of rain and the musical elements of China Gates creates a narrative of tension between their paradoxical aspects.

Conclusion

In John Adams’s China Gates, signifiers such as symmetry, rhythm, voice leading parsimony, and pitch-class and set-class repetition symbolize the “endless winter rain” that inspired Adams to compose this piece. Through this analysis, I have shown how meaning is created from the conceptual blend of musical space and rain space. In an interview with Aaron Jay Kernis, Adams expressed, “I feel that when you take a group of notes together, or some harmonic organization, or a rhythmic pulse, anything like that, that the music has its own personality, immediately, and then the really creative composer follows the implication of that material” (Adams & Kernis 1992). I believe this analysis of China Gates reflects that sentiment. Simple complexities hide beneath the surface, inviting listeners to follow their meaningful significations. Through its numerous signifiers, this piece unearths the delicate tension between the dialectical processes of rain: consistency and change, tranquility and destruction, light and dark.

---

References

Adams, John. 1983. China Gates. New York: Associated Music Publishers.

———. “China Gates: Programme Note.” Wise Music Classical. Accessed November 22, 2021. https://www.wisemusicclassical.com/work/23701/

———. “Phrygian Gates and China Gates.” John Adams – Official Website. Accessed November 19, 2021. https://www.earbox.com/phrygian-gates-china-gates/

Adams, John, and Aaron Jay Kernis. 1992. “John Adams: An Interview with Aaron Jay Kernis.” Conjunctions 19: 174–190. 

Atkinson, Sean. 2011. “Canons, Augmentations, and Their Meaning in Two Works by Steve Reich.” Music Theory Online 17(1).

Cohn, Richard. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase-Shifting Music.” Perspective of New Music 30(2): 146–177. 

Escuder, Alejandro. 2012. “John Adams y análisis de su obra “China Gates.” Unpublished manuscript. PDF. https://www.academia.edu/12581484/ JOHN_ADAMS_y_an%C3%A1lisis_de_su_obra_CHINA_GATES_

Fauconnier, Gilles, and Mark Turner. 1998. “Conceptual Integration Networks.” Cognitive Science 22(2): 133–87.

Johnson, Timothy A. 2011. John Adams’s Nixon in China: Musical Analysis, Historical and Political Perspectives. United Kingdom: Ashgate Publishing.

LA Phil. 2020. “John Adams on China Gates.” Facebook Video. LA Phil. Posted June 24. https://www.facebook.com/LAPhil/videos/john-adams-explains-china-gates-inspiration/2865110256934075/

Lakoff, George. 1993. “The Contemporary Theory of Metaphor.” In Metaphor and Thought, edited by Andrew Ortony, 2nd ed., 202–51. Cambridge: Cambridge University Press. doi:10.1017/CBO9781139173865.013.

Lankov, Jeff. 2014. “The Solo Piano Compositions of John Adams: Style, Analysis, and Performance.” PhD diss., NYU. ProQuest (AAT 3613478).

Leydon, Rebecca. 2002. “Towards a Typology of Minimalist Tropes.” Music Theory Online 8(4). 

 O’Donnell, Shaugn. 2007. “Embracing Relational Abundance,” Music Theory Online 13(3). 

Powell, Richard. 2014. “Accessible Narratives: Continuity in the Music of John Adams.” Contemporary Music Review 33(4): 390–407.

Roeder, John. 2003. “Beat-Class Modulation in Steve Reich’s Music.” Music Theory Spectrum 25(2): 275–304.

 Saintreukk. 2015. “A Brief Introduction to John Adams’ China Gates.” YouTube Video. January 15. https://www.youtube.com/watch?v=vZ3hEjlwn7o.

Sanchez-Bezar, Alexander. 2014. “Symmetry in the Music of John Adams.” Tempo 68(268): 46–60. 

Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. New York: W.W. Norton & Company.

Tarasti, Eero. 1994. A Theory of Musical Semiotics. United Kingdom: Indiana University Press.

———. 2016. “Musical Semiotics – a Discipline, its History and Theories, Past and Present.” Abstract, Semiotics and Music 36(3): 19–51.

Turner, Mark, and Gilles Fauconnier. 1995. “Conceptual Integration and Formal Expression.” Metaphor & Symbolic Activity 10(3): 183–204.

Tymoczko, Dmitri. 2004. “Scale Networks and Debussy.” Journal of Music Theory 48(2): 219–294.

UCAR Center for Science Education. “How Thunderstorms Form.” Accessed March 24, 2023. https://scied.ucar.edu/learning-zone/storms/how-thunderstorms-form

Zbikowski, Lawrence M. 1997. “Conceptual Models and Cross-Domain Mapping: New Perspectives on Theories of Music and Hierarchy.” Journal of Music Theory 41(2): 193.

———. 2017. Foundations of Musical Grammar. Oxford Studies in Music Theory. Oxford, New York: Oxford University Press.

———. 2002. Conceptualizing Music: Cognitive Structure, Theory, and Analysis. Oxford, New York: Oxford University Press.

1. For further reading on this idea, Chapter 2 of Zbikowski (2017) fleshes out the idea of “sonic analog” through Lawrence Barsalou’s theory of perceptual symbol systems and Charles Sanders Peirce’s notion of an icon.
2. 2 China Gates by John Adams. Copyright © 1983 by Associated Music Publishers, inc. International Copyright Secured. All Rights Reserved.
3. In this section, I utilize beat-class sets similarly to Cohn (1992, 146–177) and Roeder (2003, 275–304) in their analyses of Steve Reich’s phase-shifting music.
4. Though Tarasti, in A Theory of Musical Semiotics describes minimalist music as “anti-narrative,” his comment is made in reference to minimalism’s lack of beginning, middle, and end– atemporality (1994, 284). However, the form of China Gates establishes temporality. Furthermore, Tarasti remarks on minimalism’s “narrative illusion,” suggesting that narrative does in some way exist (285). Richard Powell’s article, “Accessible Narratives: Continuity in the Music of John Adams,” explores narrativity in works of Adams’s, which, like China Gates, have an “audible geography” (2014, 390).
5. There is just one differing pitch– $$\hat1$$ in Locrian (F) and $$\hat6$$ in Aeolian (E). Tymozcko (2004) refers to scales that relate in this way as “maximally intersecting.”